Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Amperímetro e Voltímetro

Ver Teoria
Exercício 8123456791011121314151617

Enunciado

Passo 1

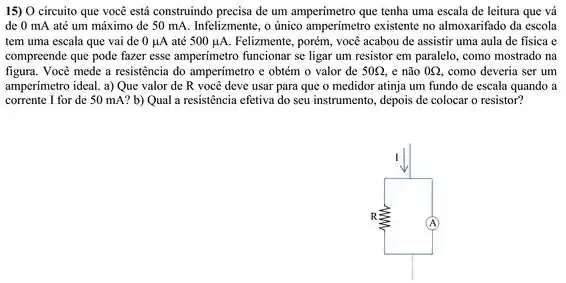
O amperímetro tem uma resistência interna em série com ele. Vamos chamar essa resistência de r . Alguns livros chama essa resistência de shuntz.

A gente liga a resistência R em paralelo com esse amperímetro e queremos o seguinte: quando a corrente máxima de 50   m A é atingida no sistema total, o amperímetro puxa apenas 500   μ A após a divisão da corrente.

Bom, a D D P na resistência R é igual à D D P na resistência r , interna ao amperímetro. Começamos então com o seguinte:

R . I R = r . I r

Passo 2

Além disso, sabemos que a soma das duas correntes é igual a 50   m A :

I R + I r = 50   m A

Passo 3

Quando essa corrente total máxima é atingida, I r = 50   μ A . Sobra para o resistor R uma corrente igual a:

I R = 50   m A - 50   μ A = 49,95   m A

Passo 4

Logo, substituindo no passo 1 :

R . 49,95   m A = 50 Ω . 50   μ A = 50 . 0,05   m A → R = 50.0,05 49,95 = 50,05   m Ω

É uma resistência pequeninha, que vai, por isso, puxar bastante corrente (afinal, a corrente se divide e tende a ir sempre pro lado com menor resistência, com o lado onde é “mais fácil” de passar, com menos “resistências” no caminho).

Passo 5

A resistência efetiva e resultante é igual à resistência em paralelo entre os dois valores:

R E Q = r . R r + R = 50 . 50,05.10 - 3 50 + 50,05.10 - 3 = 0,04999   Ω = 49,99   μ Ω

Resposta

  1. 50,05   m Ω
  2. 49,99   m Ω

Exercícios de Livros Relacionados

Na Fig. 27-14, suponha que ε = 3,0 V , r = 100 Ω , R 1 = 250 Ω e R 2 = 300 Ω . Se a resistência do voltímetro R v é 5,0 k Ω , que erro percentual o voltímetro introduz na medida da diferença de potenc
Na Fig. 27-61, o valor de R , pode ser ajustado através de um contato deslizante até que os potenciais dos pontos a e b sejam iguais. (Um teste para verificar se essa condição foi satisfeita é ligar t
Na Fig. 27-40, R 1 = 6,00 Ω , R 2 = 18,0 Ω e a força eletromotriz da fonte ideal é E = 12,0 V . Determine (a) o valor absoluto e (b) o sentido (para a esquerda ou para a direita) da corrente i 1 . (c)
Na Fig. 27-58, um voltímetro de resistência R v = 300 Ω e um amperímetro de resistência R A = 3,00 Ω estão sendo usados para medir uma resistência R em um circuito que também contém uma resistência R
Um amperímetro com diversas escalas. A resistência da bobina móvel do galvanômetro G , indicado na Figura 26.77, é igual a 48 Ω e a deflexão até o fundo da escala ocorre quando a corrente é de 0,02A .