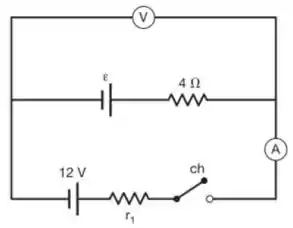
No circuito elétrico representado a seguir, o voltímetro e o amperímetro são ideais. Observa-se que, com a chave ch aberta, o voltímetro marca e, com ela fechada, o amperímetro marca . A resistência do circuito vale:
Passo 1
Quando a chave ch está aberta, não circula nenhuma corrente na parte de baixo do circuito que contém . Porém, também não passa nenhuma corrente na parte de cima do circuito onde está o voltímetro, já que ele é ideal, ou seja, tem resistência “infinita”.
Portanto, a ddp de que o voltímetro mede com a chave ch aberta é aquela devida unicamente à fonte . Por isso, o que temos nessa situação é:
Passo 2
Agora, quando a chave ch é fechada, o amperímetro vai marcar uma corrente e essa corrente vai circular apenas na malha de baixo que contém . Como o amperímetro é ideal, ou seja, tem “resistência zero”, podemos aplicar a lei das malhas e contar apenas a diferença de potencial nos outros elementos da malha.
Antes, vamos escolher o sentido para a malha e para a corrente nessa parte do circuito. Escolhemos o sentido horário tanto para a malha, quanto para a corrente , como mostramos na figura abaixo.
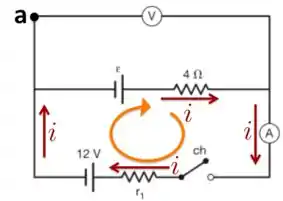
Começando do ponto e percorrendo a malha até voltar ao ponto , teremos:
Como e , temos:
Resposta
Letra d.