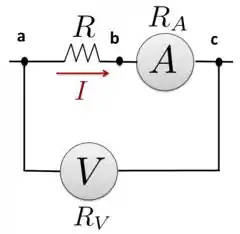
Suponha que você queira medir uma resistência desconhecida usando o circuito indicado na figura abaixo. As resistências dos instrumentos são (para o voltímetro) e (para o amperímetro). Sabendo que o voltímetro lê e o amperímetro, , responda:
- Qual é o valor de ?
- Qual é a potência dissipada em ?
Passo 1
Bom, como você viu aqui com a gente lá na teoria, um amperímetro serve para medir a corrente elétrica e é dito que ele é ideal quando não possui resistência interna, ou seja, quando . Para medir uma corrente, a gente coloca esse amperímetro de modo que a corrente, cujo valor queremos conhecer, passe dentro dele, blz?
O voltímetro, por sua vez, é utlizado para medir diferença de potencial entre dois pontos e se fala que ele é ideal quando sua resistância é infinita, isto é, e, por isso, não passa nenhuma corrente dentro do voltímetro, tranquilo? Há uma resistência infinita à passagem da corrente por dentro de um voltímetro ideal!!
Mas “A VIDA NÃO É IDEAL”, e não seria diferente com os amperímetros e voltímetros e esse é o caso que temos aqui nesse exercício. O nosso objetivo é medir o valor da resistência nesse contexto em que e !
Passo 2
a) Como o amperímetro não é ideal, ou seja, , então existe uma queda de potencial entre os pontos e quando a corrente passa dentro do amperímetro, fazendo com que (ddp entre os terminais do amperímetro!!) e aí, nessa situação, o que o voltímetro lê não é só a ddp entre os pontos e .
Nesse caso, o que o voltímetro realmente lê é o seguinte:
tranquilo?
O enunciado diz para gente que , ou seja, essa é a leitura que o voltímetro faz. Mas como o amperímetro não é ideal e tem , então,
Substituindo na expressão para , temos
Como a corrente que passa pelo resistor é , obtemos a resistência que é
Passo 3
b) Como a potência dissipada pelo resistor é dada por , encontramos, com os valores que o exercício dá, que
Resposta
- ;
- .