Um resistor de e outro de são ligados em série a uma fonte de . Considerando essa situação,
- Qual é a voltagem nos terminais de cada resistor?
- Um voltímetro conectado nos terminais do resistor de indica uma leitura de . Calcule a resistência do voltímetro.
Passo 1
Você vai perceber que esse exercício tem um pouco mais de detalhes, mas vale a pena seguir bem de perto os passos da solução aqui, porque se tiver um desses na sua prova, não vai ter erro: VOCÊ VAI MATAR O PROBLEMA SORRINDO... ;-) SEGUE FIRME...
a) Bom, vamos lá!! Nesse item, galera, a gente tem, inicialmente, apenas uma fonte que fornece uma corrente para o circuito, que é composto de dois resistores e em série, como representei para você na figura abaixo.
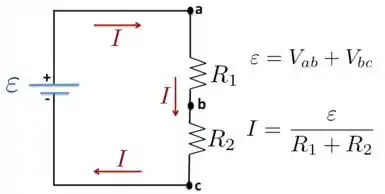
Então, como os valores das resistências e são conhecidos, assim como o valor da fem , podemos encontrar a corrente que percorre o circuito elétrico da seguinte maneira
Como essa corrente passa pelo resistor , temos a seguinte diferença de potencial entre os pontos e da figura
e entre os pontos e
Repara que temos o seguinte: , que deixei representado para você lá na figura também ;-) Até aqui, tranquilo?
Calculamos a corrente que percorre o circuito e obtivemos os valores para as diferenças de potencial e entre os resistores.
Passo 2
b) Agora, entre os teminais e do resistor colocamos um voltímetro que mede uma diferença de potencial e o que acontece nesse caso é esquematizado na figura abaixo. Foca nessa figura agora...kk
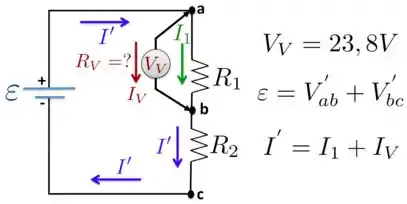
Nessa situação, a nova diferença de potencial entre o pontos e aos quais o resistor está ligado é
que é menor que a diferença de potencial que a gente tinha antes de o voltímetro ser colocado no circuito.
Então, para encontrarmos qual o valor da resistência do voltímetro, utilizaremos a seguinte expressão:
já que, nessa situação, passa alguma corrente no voltímetro, uma vez que o voltímetro tem uma resistência !!. Mas fica ligado, pq ainda não conhecemos o valor da corrente !!
Para chegarmos lá, a gente precisa se lembrar que, por causa do voltímetro inserido no circuito, a corrente que entra no ponto não é mais !! Mas, então, qual é a nova corrente ’ que temos nesse caso?
Como a fonte fornece uma fem de valor fixo, , e a diferença de potencial , então a nova diferença de potencial entre os terminais e do resistor é
que dá para gente o novo valor para a corrente
Mas essa ainda não é a corrente que passa pelo voltímetro!! Da figura, você percebe que a corrente que entra pelo ponto deve ser igual à corrente que sai do ponto ; por isso, temos que
A nova corrente que passa pelo resistor pode ser obtida como
Daí, então, basta substituir na expressão para e obter seu valor
Agora, ficou fácil, né? A resistência é
Repara que, apesar de ser uma resistência de valor grande, não é uma resistência “infinita”, o que faz com que a corrente que passa através do voltímetro seja !!
Resposta
- ; ;
- .