(a)
(b)
(c)
(d)
(e)
![]()
(a) ;
(b)
(c)
(d)
(e)
Passo 1
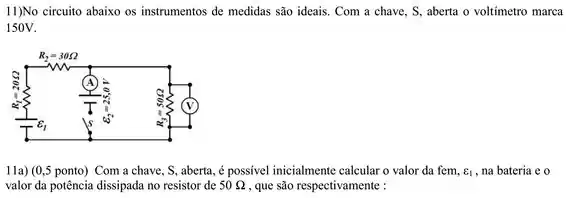
11a) A questão diz que os instrumentos de medida são ideais. Então:
- O amperímetro conta como um curto-circuito
- O voltímetro conta como um circuito aberto
Passo 2
Calcular a corrente elétrica quando a chave está aberta. O lance é dividir o potencial pela soma das três resistências, que é a resistência equivalente do circuito:
Passo 3
Essa corrente multiplicada pela resistência nos dá o potencial em cima desse resistor, que é medido pelo voltímetro e vale :
E já eliminamos as letras (B), (C) e (D).
Passo 4
A potência em cima desse resistor pode ser calculada por:
Passo 5
11b) Quando a chave é fechada, o potencial em cima do resistor passa a valer pois a bateria liga os dois extremos desse resistor, em paralelo com o voltímetro.
Por isso, a potência dissipada em passa a valer:
E só com esse passo a gente já elimina tudo e pode marcar a letra (B) ;) O Passo 6 é importante para fixar a matéria e para ver o que fazer caso você não perceba isso na hora da prova OK?
Passo 6
Na letra (a) a gente viu que . Vamos usar essa informação aqui.
Você pode olhar para cada malha em separado, calcular a corrente em cada uma delas e sobrepor no final as duas correntes.
Dessa forma a gente encontra a corrente no ramo do meio do circuito. Ficou confuso? Vamos ver isso mais de perto.
Primeiro: no resistor a corrente vale:
E essa corrente anda de cima para baixo em , do maior para o menor potencial. Essa corrente passa no amperímetro de baixo para cima.
Mas não é só essa corrente que vai estar em cima do amperímetro: a parte esquerda do circuito também influencia o resultado.
Em cima de em série com existe uma diferença de potencial igual a:
Esse potencial a gente divide pela resistência equivalente :
Essa corrente sai do maior potencial e anda em direção ao menor potencial de . Por isso ela passa no amperímetro de cima para baixo.
Passo 7
Agora vamos olhar as duas correntes que encontramos:
- passa no amperímetro de baixo para cima
- passa no amperímetro de cima para baixo
A corrente resultante é, então de de cima para baixo.
De qualquer forma, vou repetir, só com o passo 5 já poderíamos ter resolvido a questão! Além disso, essa parte de calcular a corrente pedia que você tivesse calculado o potencial corretamente na questão anterior.
Por isso, essa parte é mais arriscada. É bem importante você levar essa malandragem para a prova.
Resposta
11a) (a) .
11b) (b)