Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Amperímetro e Voltímetro

Ver Teoria
Exercício 2134567891011121314151617

Enunciado

Na figura abaixo, determine a leitura do amperímetro para ε = 5 V (fonte ideal) , R 1 = 2 Ω ,   R 2 = 4 Ω   e   R 3 = 6 Ω .

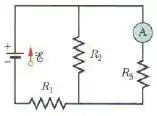
Passo 1

Se ele está nos pedindo a medição do amperímetro, ele está pedindo a corrente que passa ali, certo?

Então o que temos que fazer é calcular a corrente que passa naquele ramo! #VamoQueVamo!

Passo 2

A corrente sempre vai do menor para o maior potencial, logo o sentido da corrente será esse aqui, oh!

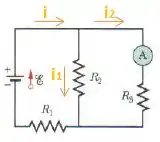
Passo 3

Aplicando a Lei dos Nós no nó em cima de R 2 , teremos:

i = i 1 + i 2

Tranquilo até aí, né?

Agora aplicando a Lei das Malhas, teremos:

Na esquerda.

ε - i 1 R 2 - i R 1 = 0

Na direita.

- R 3 . i 2 + i 1 R 2 = 0

Passo 4

Beleza, 3 equações, 3 incógnitas,é só resolver o sisteminha!

i 2 = i - i 1

- R 3 . i - i 1 + i 1 R 2 = 0

- R 3 i + R 3 i 1 + i 1 R 2 = 0

i = i 1 R 2 + R 3 R 3

Aplicando agora na equação da malha da esquerda, vamos ter:

ε - i 1 R 2 - i 1 R 2 + R 3 R 3 R 1 = 0

ε = i 1 R 2 . R 3 + R 1 . R 2 + R 3 R 3

i 1 = ε . R 3 R 2 . R 3 + R 1 . R 2 + R 3 = 5.6 4.6 + 2 [ 4 + 6 ] = 0,6818 A

Passo 5

A gente descobriu lá na Lei das Malhas na direita, que:

i 2 = i 1 R 2 R 3

Logo

i 2 = 0,6818.4 6 = 0,45 A

Resposta

i 2 = 0,45 A

Exercícios de Livros Relacionados

Na Fig. 27-14, suponha que ε = 3,0 V , r = 100 Ω , R 1 = 250 Ω e R 2 = 300 Ω . Se a resistência do voltímetro R v é 5,0 k Ω , que erro percentual o voltímetro introduz na medida da diferença de potenc
Na Fig. 27-61, o valor de R , pode ser ajustado através de um contato deslizante até que os potenciais dos pontos a e b sejam iguais. (Um teste para verificar se essa condição foi satisfeita é ligar t
Na Fig. 27-40, R 1 = 6,00 Ω , R 2 = 18,0 Ω e a força eletromotriz da fonte ideal é E = 12,0 V . Determine (a) o valor absoluto e (b) o sentido (para a esquerda ou para a direita) da corrente i 1 . (c)
Na Fig. 27-58, um voltímetro de resistência R v = 300 Ω e um amperímetro de resistência R A = 3,00 Ω estão sendo usados para medir uma resistência R em um circuito que também contém uma resistência R
Um amperímetro com diversas escalas. A resistência da bobina móvel do galvanômetro G , indicado na Figura 26.77, é igual a 48 Ω e a deflexão até o fundo da escala ocorre quando a corrente é de 0,02A .