Exercícios Resolvidos de Amperímetro e Voltímetro

Exercício 9 1 2 3 4 5 6 7 8 10 11 12 13 14 15 16 17

Enunciado

No circuito abaixo os instrumentos de medidas são ideais. Com a chave aberta, o voltímetro marca .

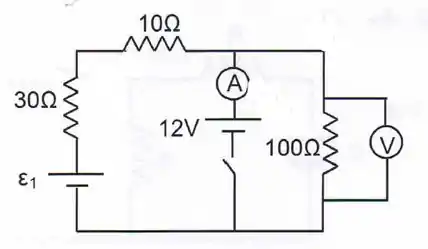
I - Com a chave aberta é possível inicialmente calcular o valor da fem na bateria e o valor da potência dissipada no resistor de , que são respectivamente:

(a)

(b)

(c)

(d)

(e)

II - Com a chave fechada o valor lido no amperímetro e o valor da potência dissipada no resistor de é igual a:

(a)

(b)

(c)

(d)

(e)

Passo 1

I – No resistor da direita temos que, pela informação do voltímetro:

Como , então

Caminhando pelo circuito, temos:

Substituindo o valor de :

Passo 2

E para achar a potência, é simples:

Passo 3

II –

Agora vamos fechar a chave! Dessa vez temos 3 correntes como no desenho

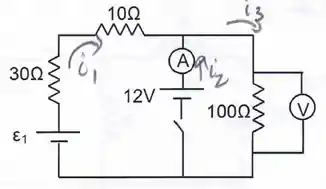
Com a chave fechada a ddp sobre a resistência de é de , assim, a corrente que passa pelo ramo da direita é dada por:

Agora percorrendo a malha da esquerda:

Pela lei dos nós:

Como já temos e

E essa é a corrente no amperímetro. O fato dela ser negativa indica que ela está no sentido contrário que a gente convencionou, ou seja, para baixo.

Passo 4

Para encontrar a potência:

Resposta

a) (c)

b) (e)

Exercícios de Livros Relacionados

Na Fig. 27-14, suponha que ε = 3,0 V , r = 100 Ω , R 1 = 250 Ω e R 2 = 300 Ω . Se a resistência do voltímetro R v é 5,0 k Ω , que erro percentual o voltímetro introduz na medida da diferença de potenc

Na Fig. 27-61, o valor de R , pode ser ajustado através de um contato deslizante até que os potenciais dos pontos a e b sejam iguais. (Um teste para verificar se essa condição foi satisfeita é ligar t

Na Fig. 27-40, R 1 = 6,00 Ω , R 2 = 18,0 Ω e a força eletromotriz da fonte ideal é E = 12,0 V . Determine (a) o valor absoluto e (b) o sentido (para a esquerda ou para a direita) da corrente i 1 . (c)

Na Fig. 27-58, um voltímetro de resistência R v = 300 Ω e um amperímetro de resistência R A = 3,00 Ω estão sendo usados para medir uma resistência R em um circuito que também contém uma resistência R

Um amperímetro com diversas escalas. A resistência da bobina móvel do galvanômetro G , indicado na Figura 26.77, é igual a 48 Ω e a deflexão até o fundo da escala ocorre quando a corrente é de 0,02A .