O circuito indicado na figura abaixo denomina-se ponte de Wheatstone e é usado para determinar uma resistência desconhecida por comparação com três resistores , e , cujam resistências podem variar. Para cada conjunto, a resistência de cada um desses resistores pode ser conhecida com precisão. Com as chaves e fechadas, fazemos variar essas resistências até que a corrente indicada no galvanômetro seja igual a zero; dizemos, então, que a ponte está equilibrada.
- Mostre que, quando isso ocorre, a resistência desconhecida é dada por ?
- Sabendo que o galvanômetro indica deflexão igual a zero quando , e , qual é o valor da resistência desconhecida ?
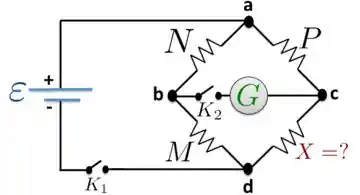
Passo 1
Como o exercício comenta, esse aparato serve para medir uma resistência desconhecida . Como as outras resistências do circuito são variáveis, à medida que vão sendo mudadas de forma controlada e conhecida, o valor da corrente que passa através do galvanômetro (amperímetro) vai mudando e na figura abaixo desenho um pouco do que tá acontecendo e que vai ser útil para analisarmos os próximos passos.
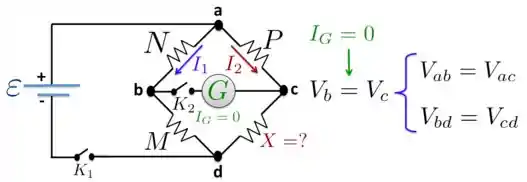
Quando a corrente que passa pelo amperímetro é , como conhecemos os valores das resistências , e referentes à essa situação, podemos determinar o valor da resistência através da expressão que temos que provar...
Bom, vamos provar aquela expressão primeiro...Então, mãos à obra, galera...!!!
Passo 2
a) Na figura acima, desenhei para você o que tá rolando nesse exercício e vou tentar colocar o que acontece lá numerando as situações da seguinte maneira:
- implica que os pontos e tem o mesmo potencial: , ou seja, como não tem corrente através do amperímetro (galvanômetro!), não tem queda de potencial entre esses pontos!! Fechou? Isso é crucial, hein?!! Fica de olho...
- Como , então: . Isso significa, olhando lá para figura, que a gente tem o seguinte:
- Também porque , obtemos que: . Com isso, chegamos a
Repara que só podemos fazer essas afirmações acima se !!!!
Se a gente iguala esses duas últimas expressões para a corrente dos itens 2) e 3), advinha o que acontece?? Tchãããrããã….
Feliz ou não?? Kkk
Acabamos de chegar, com as etapas 1), 2) e 3) acima (válidas quando !!), na expressão que queríamos demonstrar para a resistência desconhecida :
Repara, ainda, que em nenhum momento a gente precisou conhecer o valor da fem do circuito!!! Ou seja, dado uma fem, uma bateria por exemplo, vamos variando as resistências , e até que a corrente no amperímetro (galvanômetro!) seja NULA: ! Quando isso acontece, anotamos os valores das resistências para esse caso e, utilizando essa expressão que encontramos agora, obtemos o valor da resistência , AGORA CONHECIDA….\0/\0/\0/
Passo 3
b) Esse item não tem segredo, porque agora é só substituir os valores fornecidos no enunciado do exercício para matar de vez a questão:
Resposta
- Demonstração de: