Determinar o ângulo entre os planos
Passo 1
Bom, do plano eu sei o vetor normal!
Mas e o vetor normal de ??
Pensa comigo, galera. O plano é formado por um vetor diretor da reta do eixo e um vetor diretor da reta do eixo :
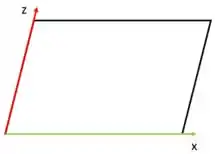
Então se nós fizermos o produto vetorial entre e , vamos obter um vetor perpendicular a eles, ou seja, um vetor normal ao plano!
Considerando e , temos:
Logo,
Passo 2
Agora é só completar a fórmula!
Calculando os termos:
Colocando os valores na fórmula, temos: