Obtenha uma parametrização para a seguinte superfície:
Passo 1
Primeira pergunta, vocês lembram que superfície é essa? Se não lembram eu vou dar uma ajuda, é um hiperbolóide de uma folha! Alguma coisa assim oh:
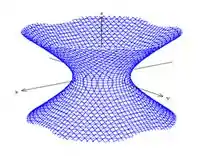
Sacou?
E como ele é formado? Ele é uma hipérbole rotacionada em torno de um eixo!!! No caso, é rotacionada em torno do eixo que está com o sinal negativo (o ). Então estamos parametrizando uma superfície de revolução 😉
Vamos usar como curva a parte de da hipérbole no plano :
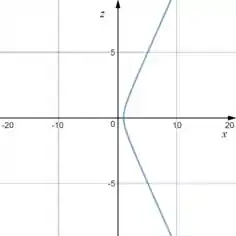
Passo 2
Show, próximo problema! Já sabemos que essa superfície é formada pela revolução de meia hipérbole. Mas como que é a parametrização de uma hipérbole?!?!
Pois é, temos que lembrar disso na hora também, então puxe todos os seus conhecimentos de parametrização de curvas agora! A parametrização é essa aqui oh:
Sendo que essa é só a parte com positivo da hipérbole.
Então para a nossa hipérbole , temos:
Além disso, como e são parecidos quando rodamos em torno de , vai aparecer um no também!
Passo 3
Pra finalizar rotacionamos isso em torno do eixo e ficamos com: