Parametrize a porção da esfera que não se encontra no interior do paraboloide .
Passo 1
Primeiramente, sabemos que a parametrização de uma esfera é melhor em coordenadas esféricas, então já podemos atacar com a seguinte parametrização:
Onde . Seguindo, temos:
Substituindo :
Podemos seguir com a limitação da esfera, que é estar fora do paraboloide.
Passo 2
Um ponto está fora do paraboloide se ele respeita a inequação:
Como podemos averiguar pelo gráfico:
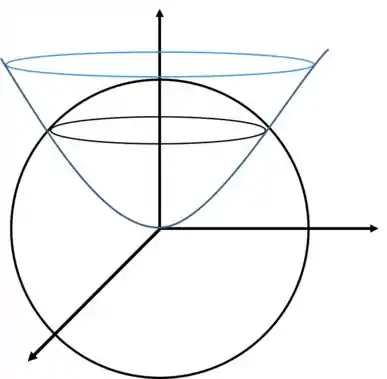
Portanto, arrumando malandramente, somamos em ambos lados:
As raízes são:
Mas como temos um paraboloide deve ser sempre positivo, então eles se encontram em E assim:
De resto o , por sua definição, pode ir até , então:
O não tem restrições, com exceção daquela convencionada pela trigonometria:
Resposta
Exercícios de Livros Relacionados
Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u ,
Determine se os pontos PeQ estão na superfície dada. r u , v = u + v ,u - 2 v , 3 + u - v P 4 , - 5,1 , Q ( 0,4 , 6 )
Determine as equações paramétricas da superfície obtida pela rotação da curva y = e - x , 0 ≤ x ≤ 3 , em torno do eixo x e use-as para traçar o gráfico da superfície.
O que acontecerá com o tubo espiral do Exemplo 2 (veja a Figura 5 ) se substituirmos cos u por sen u e sen u por cos u ?O que acontecerá se substituirmos cos u por cos 2 u e sen u por se
Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. x = c