Seja a parte do paraboloide limitada pelo plano . Uma parametrização da superfície é:
a)
b)
c)
d)
e)
Passo 1
Queremos parametrizar o paraboloide né? Ele tem essa equação:
Como ela tá escrita como uma função de e explícita:
A gente pode parametrizar ela assim:
Mas isso não está nenhum pouco parecido com as alternativas né? E ainda falta achar o domínio. Então vamos continuar!
Passo 2
Vamos fazer um gráfico do que está acontecendo e achar esse domínio:
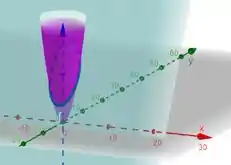
Nosso paraboloide na real só vai até a curva azulzinha (a interseção com o plano). Se a gente achar a projeção dessa curva em , a gente acha a região em que nosso paraboloide está dentro, né?
Para achar essa projeção em , é só a gente igualar os valores de das duas superfícies que a gente tem:
Completando quadrados, achamos:
Isso é uma circunferência de raio e com centro em . Já que nossa superfície está dentro dela, podemos escrever que:
Esse vai ser nosso domínio.
Passo 3
Agora repara que nosso domínio é um círculo, nada mais justo do que reescrever ele em coordenadas polares, né?
Vamos desenhar o gráfico desse cara:
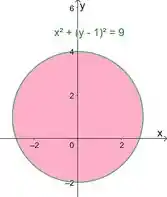
Como o nosso centro do domínio não está na origem mas em , vamos usar as coordenadas polares descolocadas para esse centro, somando na coordenada convencional, assim:
E como se os nossos eixos de e fossem deslocados, e a origem deles ficassem no centro do círculo. Quando isso acontece, dá a volta completa em torno da origem para passar pelo círculo todo.
Vamos substituir as expressões das mudanças polares na nossa inequação do domínio para limitar :
Daí a gente pode tirar que:
Passo 4
Vamos substituir essa mudança de coordenadas na nossa parametrização lá do começo:
E a gente tem isso na letrinha c, junto com o domínio que a gente tinha achado:
Então essa é a nossa parametrização!
Resposta
Letra c