A norma da projeção ortogonal do vetor na imagem de uma matriz é igual a 3. Calcule a norma da projeção ortogonal de no núcleo de
(a)
(b)
(c)
(d)
Passo 1
Primeiramente temos que lembrar que , então queremos a norma da projeção ortogonal de no complemento ortogonal da imagem da matriz.
Vamos supor que a imagem da matriz é um plano e portanto seu complemento ortogonal vai ser uma reta para visualizarmos melhor:
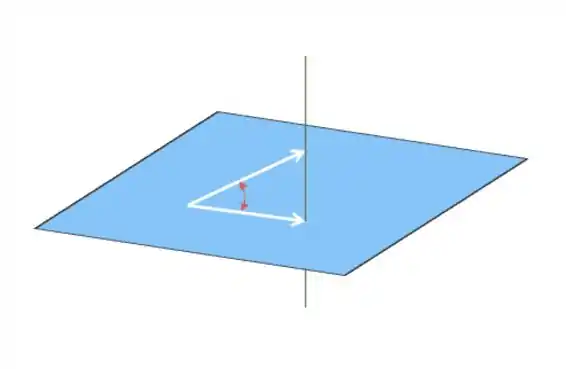
Bom, aí temos o plano que é a , a reta perpendicular a ele que vai ser seu complemento ortogonal, o vetor e sua projeção no plano! Já dá para visualizar o que queremos:
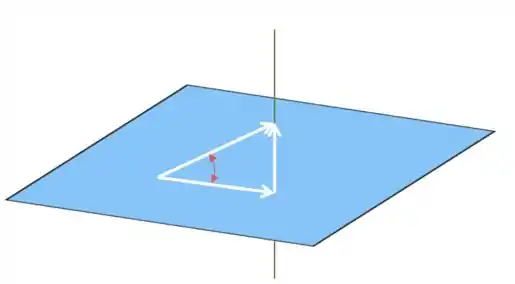
Isso formou um triângulo retângulo!!
Passo 2
Nós temos o módulo da projeção, as coordenadas de , que podemos utilizar para poder achar seu módulo, e queremos o módulo da outra projeção. É só usar Pitágoras:
Primeiro vamos achar o módulo do vetor
Agora sim:
Resposta
b