Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Condução de Calor

Ver Teoria
Exercício 36123456789101112131415161718192021222324252627282930313233343537

Enunciado

Uma barra de seção transversal constante de 1   c m 2 de área tem 20   c m de comprimento, dos quais 10   c m de alumínio e 10   c m de ferro. A extremidade de alumínio está em contato com um reservatório térmico a 100 ° C , e a de ferro com outro, a 0   ° C . A condutividade térmica do alumínio é 0,48   c a l / s . c m ° C e a do ferro é 0,16   c a l / s . c m ° C .

  1. Qual é a expressão do calor transferido por unidade de tempo através da barra de alumínio, em função da diferença de temperatura entre as extremidades da barra de alumínio?
  2. Qual é a expressão do calor transferido por unidade de tempo através da barra de ferro, em função da diferença de temperatura entre as extremidades da barra de ferro?
  3. No equilíbrio térmico, qual é a temperatura da barra na junção entre o alumínio e o ferro?
  4. Se o reservatório térmico de 0 ° C é uma mistura de água com gelo fundente, qual é a massa de gelo que se derrete por hora? O calor latente de fusão do gelo é 80 c a l g .

Passo 1

Bom galera, nesse tipo de exercício é legal a gente fazer um esquema, para termos uma melhor visualização do que está ocorrendo no nosso sistema.

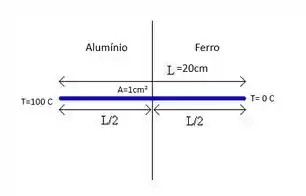
Onde:

L = 20 c m

k a = 0,48 c a l s . c m ° C

k f = 0,16   c a l / s . c m ° C

Agora que já temos uma representação gráfica do nosso enunciado, vamos desenvolver uma expressão para o calor transferido por unidade de tempo através da barra de alumínio. A taxa de condução de calor é o quanto de calor passa por um material por unidade de tempo e é representado por:

H = Q / ∆ t

Podemos calcular a taxa de condução de calor da seguinte maneira:

H = k a l A a l T a l - T 1 L ,

Onde: k é a condutividade térmica e A é a área por onde o calor se propaga.

Passo 2

Vimos no passo anterior que a taxa de transferência de calor é representada por:

H = k a T 2 - T 1 L ,

sendo T 1 a temperatura de 0 ° C que a barra de ferro está em contato, temos portanto:

H f e = Q f e t = k f e A f e T f e - T 0 L

Passo 3

No equilíbrio, temos que H a l = H f e , vamos então desenvolver as equações dessa igualdade:

k a l A a l T a l - T 1 L = k f e A f e T f e - T 0 L

k a l T a l L a l - K a l T 1 L a l = k f e T f e L f e - K f e T 0 L f e

T = k a l T a l L a l + k f e T f e L f e k a l L a l + k f e L f e = 048 × 373 10 + 0,16 × 273 10 0,16 10 + 0,48 10 = 348 K

Passo 4

Sabemos que:

Q f e t = k f e A f e T f e - T 0 L

∴

Q f e = t k f e A f e T f e - T 0 L = 3600 × 0,16 × 1 × 348 - 273 10 = 4320   c a l

O enunciado diz que o calor latente do gelo é 80 c a l / g , logo:

m = Q c L = 4320 80 = 54 g

Resposta

a) H = k a l A a l T a l - T 1 L

b)   H f e = k f e A f e T f e - T 0 L

c)348K

d) 54g

Exercícios de Livros Relacionados

Um carpinteiro constrói uma porta de madeira maciça com dimensões de 2,0m × 0,95m × 5,0c m . Sua condutividade térmica é k = 0,120 W / m ⋅ K . A película de ar sobre a superfície interna e a película
Pingentes de gelo. A água cobre a superfície de um pingente de gelo ativo (em processo de crescimento) e forma um tubo curto e estreito na extremidade do eixo central (Figura). Como a temperatura da i
A figura mostra uma parede feita de quatro camadas, de condutividades térmicas k 1 = 0,060 W m . K , k 3 = 0,040 W m . K e k 4 = 0,12 W m . K ( k 2 não é conhecida). As espessuras das camadas são L 1
( a ) Calcule a taxa com a qual o calor do corpo atravessa a roupa de um esquiador em regime estacionário, a partir dos seguintes dados: a área da superfície do corpo é 1,8m 2 ; a roupa tem 1,0c m de
Efeito Leidenfrost. Quando se deixa cair uma gota d’água em uma frigideira cuja temperatura está entre 100 ° C e 200 ° C , a gota dura menos de 1s . Entretanto, se a temperatura da frigideira é maior,