Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Condução de Calor

Ver Teoria
Exercício 31245678910111213141516171819202122232425262728293031323334353637

Enunciado

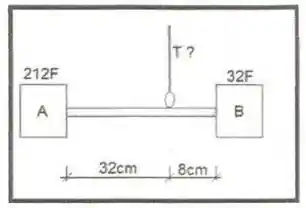
Temos uma barra de alumínio de comprimento 40 c m e área transversal de 10 c m 2 isolada com cortiça; um termômetro fixo na barra calibrado em Farhenheit, e dois dispositivos, A e B   que proporcionam nas extremidades da barra, as temperaturas 212 ° F e 32 ° F , respectivamente. Considerando a intensidade da corrente térmica constante ao longo da barra, determina a temperatura registrada no termômetro, sabendo que ele se encontra a 32   c m do dispositivo A .

Dado: k a l u m í n i o = 237 W / m . K

Passo 1

Bom galera, nessa questão usaremos o conceito de condução de calor. O pulo do gato dessa questão será considerar o princípio da conservação da energia.

Se a energia não se perde, a taxa de condução deve ser a mesma ao longo de toda a barra, certo?

E esse é o pulo do gato. Vamos igualar as taxas de condução de calor para descobrir a temperatura do termômetro.

Mas antes, vamos converter os valores das extremidades para Kelvin:

T K - 273 5 = T F - 32 9  

  T K - 273 5 = 212 - 32 9

T K = 373   K = T 1  

∴

Para T 2 agora

T K - 273 5 = T f - 32 9  

  T K - 273 5 = 32 - 32 9  

T K = 273   K = T 2  

Passo 2

A gente quer achar a temperatura do ponto onde está o termômetro. Vamos chama-la de T x .

Vamos escrever a primeira taxa, a referente ao comprimento de 32 c m :

H 1 = k a l u m í n i o . A T 1 - T x 32 x 10 - 2

H 1 = 237.10.10 - 4 373 - T x 32 x 10 - 2

Vamos deixar assim por enquanto.

E a taxa da segunda parte será:

H 2 = k a l u m í n i o . A T x - 273 8 x 10 - 2

H 2 = 237.10.10 - 4 T x - 273 8 x 10 - 2

Passo 3

Igualando as duas taxas:

H 1 = H 2  

  237.10.10 - 4 373 - T x 32 x 10 - 2 = 237.10.10 - 4 T x - 273 8 x 10 - 2  

373 - T x 4 = T x - 273

373 - T x = 4 T x - 1092  

T x = 293 K

Resposta

T x = 293 K

Exercícios de Livros Relacionados

Um carpinteiro constrói uma porta de madeira maciça com dimensões de 2,0m × 0,95m × 5,0c m . Sua condutividade térmica é k = 0,120 W / m ⋅ K . A película de ar sobre a superfície interna e a película
Pingentes de gelo. A água cobre a superfície de um pingente de gelo ativo (em processo de crescimento) e forma um tubo curto e estreito na extremidade do eixo central (Figura). Como a temperatura da i
A figura mostra uma parede feita de quatro camadas, de condutividades térmicas k 1 = 0,060 W m . K , k 3 = 0,040 W m . K e k 4 = 0,12 W m . K ( k 2 não é conhecida). As espessuras das camadas são L 1
( a ) Calcule a taxa com a qual o calor do corpo atravessa a roupa de um esquiador em regime estacionário, a partir dos seguintes dados: a área da superfície do corpo é 1,8m 2 ; a roupa tem 1,0c m de
Efeito Leidenfrost. Quando se deixa cair uma gota d’água em uma frigideira cuja temperatura está entre 100 ° C e 200 ° C , a gota dura menos de 1s . Entretanto, se a temperatura da frigideira é maior,