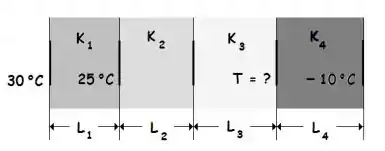
A figura mostra (em seção transversal), uma parede composta de quatro camadas, com condutividade térmica , e (não é conhecida). As espessuras das camadas são , e não é conhecida). A transferência de energia através da parede é estacionária. Qual a temperatura na interface entre as camadas 3 e 4?
Passo 1
Bom, galera, primeiramente, o que significa dizer que há uma transferência de energia estacionária?
A ideia de um sistema estacionário é que não varia com o tempo e isso geralmente está ligada ao conceito de conservação!
Logo, isso quer dizer que todo o calor que entra também sai! Nesse problema, isso quer dizer que as taxas de transferência de calor das camadas são iguais! Então, sendo a taxa de transferência de calor que é dada por:
Onde:
: Condutividade térmica.
: Área da transferência de calor.
: Comprimento do condutor
: Diferença de temperatura, tal que ;
Teremos:
Passo 2
Mas saber que as taxas são iguais nos ajuda em quê? Bom, o problema nos diz que o sistema tem várias coisas desconhecidas (. Só que a gente só quer descobrir o !
Repare que o a temperatura é a temperatura da extremidade esquerda da camada 4. Se a gente soubesse essa temperatura, daria pra calcular a taxa de transferência dessa camada, certo?
Ela ficaria assim:
Por que calculamos a diferença de temperatura assim? Bom, como o calor flui da maior temperatura para a menor, ao menos de forma natural, a gente espera que seja maior que . (Lembra que na fórmula é maior que ?).
Aí vem o pulo do gato: Como as taxas de calor são iguais, vamos comparar essa taxa com a incógnita a uma taxa conhecida. A taxa que podemos calcular facilmente é a da camada 1. Então:
Pronto! Agora vamos resolver essa equação para achar ! (:
Passo 3
Vamos resolver a equação agora. Os dados que temos são:
Na equação ficará:
Cortando o e fazendo simplificações:
Perceba que . O que era o esperado (: