Um bloco de gelo de massa inicialmente a está a uma distância de uma fonte de calor mantida a uma temperatura constante onde (ver figura abaixo). Entre o gelo e a fonte de calor, existe uma material cuja condutividade térmica é e cuja área transversal é Considere que o condutor tem baixa capacidade térmica, de forma que podemos desprezar o calor necessário para aquecê-lo. Sendo o calor de fusão da água e o calor específico da água , faça o que é pedido abaixo. Demonstre seus resultados de forma clara e organizada, deixando sua resposta apenas em função dos parâmetros definidos no enunciado (ou seja, não substitua os valores).

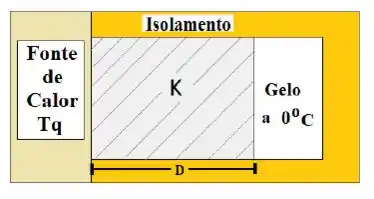
a)Ache uma expressão para o tempo necessário para que todo o gelo derreta e se torne água a .

b)Determine quanto tempo leva para que a água a seja aquecida até uma temperatura , onde .[Dica: Note que a diferença de temperatura entre as extremidades do condutor deixará de ser constante. Use e realize uma integral.]

Esse calor precisa ser igual ao que? Precisa ser igual ao calor necessário pra derreter o gelo!!!!

E esse calor é dado por:

Assim:

b)

Agora o cnário muda: Não temos mais uma temperatura constante, como no exemplo anterior. Pelo contrário, agora a temperatura varia de acordo com o calor que a água recebe.

Quanto maior a temperatura, mais se aproxima de e menor é a potência transferida, certo? Show de bola. Vamos, então, definir o calor infinitesimal trocado:

Além disso, como no exemplo anterior, esse calor é igual ao calor fornecido pela fonte de potência:

Perceba que ao invés de usarmos usamos Além disso, veja que é uma variável. Assim:

Manipulando a expressão:

Integrando os dois lados, e considerando e como temperatura e tempo inicial:

Usando

Assim:

Chamando