Dois cilindros de metal de mesma seção reta de área A, com coeficientes de condutividade térmica , e comprimentos estão unidos por uma de suas extremidades. A extremidade livre do cilindro com é mantida a temperatura , já a do outro cilindro é
mantida a temperatura . No regime estacionário, quando o fluxo de calor é independente da posição ao longo dos cilindros, qual é a temperatura na junção dos cilindros e a quantidade de calor Q que atravessa a barra num intervalo de tempo ?
- ,
- ,
- ,
- ,
- ,
- ,
Passo 1
Como temos dois metais unidos por uma extremidade, estamos tratando de uma associação em série de condutores, como na figura abaixo.
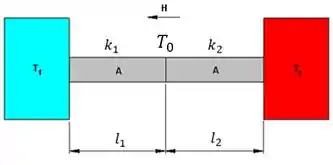
Usando a fórmula da taxa de condução de calor:
Podemos descobrir quanto calor flui no sistema, pois
Pelo princípio de conservação de energia, todo o calor que entra por um dos metais, tem que sair pelo outro metal. Ou seja,
Se usarmos a igualdade acima podemos descobrir qual a temperatura no ponto de encontro dos metais ().
Passo 2
O calor que flui no sistema pode ser escrito em função do metal 1 ou do metal 2.
O metal 1 está entre as temperaturas e :
O metal 2 está entre as temperaturas e :
Ou seja, o calor em todas as alternativas estão corretas. Não conseguimos excluir nenhuma ainda. :(
Mas não desanime!
Passo 3
Pela conservação de energia,
Cortando e rearranjando,
Considerando arbitrariamente que , (se você considerar o contrário também dá certo!),
Resposta
- ,