Dois cilindros longos, finos, sólidos e idênticos são utilizados para conduzir calor de um reservatório quente para outro frio. Sabendo que na configuração à esquerda (na figura abaixo) a taxa de transferência de calor é , qual o valor da taxa de transferência de calor para a configuração da direita?
Passo 1
Bom, a taxa de transferência de calor de um condutor é dada por:
Onde é a condutividade térmica do material (que é a mesma para os dois cilindros), é a área do condutor, é a variação de temperatura dos reservatórios e é o comprimento do condutor.
Vamos olhar para as duas configurações, onde a da esquerda vai ter uma transferência dada por:
E a da direita vai ter a seguinte taxa de transferência...
Passo 2
Primeiro, vamos encontrar a taxa de transferência para a configuração da esquerda:
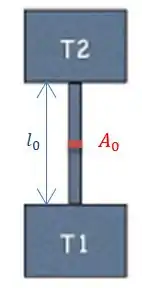
Então vamos considerar que vale:
Agora vamos olhar para a configuração da direita e ver o que ela tem de diferente...
Passo 3
Olhando para as duas configurações, vemos que:
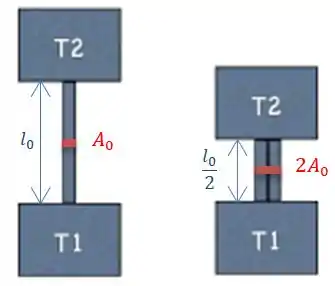
Na segunda configuração, o comprimento por onde o calor é propagado é a metade da primeira:
Mas com relação à área da seção reta por onde o calor é propagado, agora temos o dobro da área.
Pensa aqui, ao colocar as duas barrinhas, lado a lado, o comprimento do caminho que o calor vai percorrer diminuiu a metade. No entanto, a área desse caminho foi dobrada, por que agora temos duas barrinhas lado a lado.
Agora vamos pegar a fórmula da transferência de calor da segunda configuração:
E substituir os valores que acabamos de encontrar...
Logo, vamos ter:
E escrevendo isso em termos de
Com isso, temos a letra !