Classifique as seguintes cônicas degeneradas:
Passo 1
Nesse exercício temos que classificar as cônicas degeneradas que nos são dadas. Lembrando que as cônicas degeneradas são todas aquelas que falamos na teoria, ou seja: origem, retas, circunferência, entre outras. Basicamente, qualquer cônica que não seja elipse, hipérbole ou parábola.
Passo 2
a)
A solução da equação acima é:
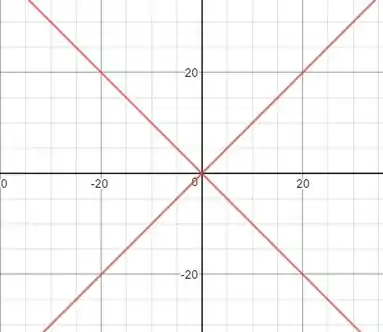
Essa solução nada mais é que um conjunto de retas, ou seja, as retas:
O exercício não pede, mas esboçando:
Passo 3
b)
Nesse item temos tanto quanto elevados ao quadrado e a soma deles dando zero. A única solução possível é que e sejam zero, logo:
Então, nossa solução representa a origem do sistema cartesiano.
Passo 4
c)
Agora, para que nossa equação seja válida temos que ter:
Porém, esse resultado é impossível nos reais já que temos a soma de quadrados, e sabe-se que qualquer número real ao quadrado é positivo, então temos a soma de dois números positivos tendo que dar . Pela inviabilidade de solução, temos que a expressão representa o VAZIO.
Passo 5
d)
E agora, como fazemos??
Bem, vamos tentar ajeitar a expressão completando quadrados para que então possamos concluir algo. Completando quadrados teremos:
Nossa equação representa a reta
Passo 6
d)
Ufa!! É a última!!

Para achar qual cônica é, vamos novamente completar quadrados. Teremos:
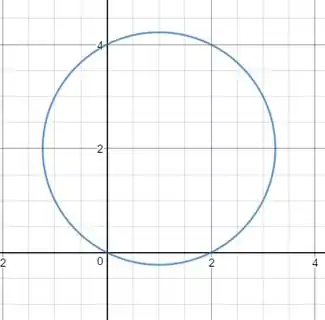
Olha, é uma circunferência!! Com centro em e raio
Caso você tenha curiosidade de como é a circunferência fizemos um esboço.