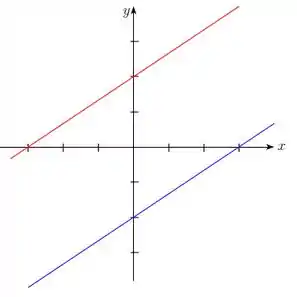
Identifique e esboce, no plano , a cônica de equação
Passo 1
Esse exercício pode ser mais fácil do que a gente pensa se percebermos que na nossa equação temos um quadrado perfeito, olha:
ou
Então, temos essas duas retas:
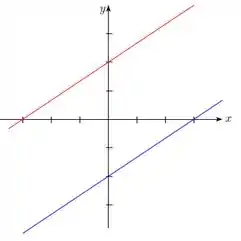
Nesse caso temos uma parábola degenerada, o que formou duas retas paralelas ;)
Resposta
Parábola degenerada: ou
Exercícios de Livros Relacionados
A equação representa uma cônica degenerada. Identificá-la e esboçar o gráfico, quando possível. x 2 + y 2 + 2 x y - 8 = 0
Efetuar uma rotação nos eixos coorenados a fim de eliminar o termo em x y . Identificar a cônica e escrever sua equação no sistema x ' O y ' obtido após a rotação. Esboçar o gráfico. x 2 + y 2 + 4 x y
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 6 . 4 x y + 3 x 2 = 4
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 7 . x 2 + 2 x y + y 2 - 8 x + 8 y = 0
Determinar a equação reduzida referida ao sistema X O ' Y e o gênero da cônica representada pela equação dada a seguir. Esboçar o gráfico. 4 x 2 + 6 x y - 4 y 2 + 20 x - 20 y - 19 = 0