Calcule a integral de linha
Onde é região definida entre as curvas e . Considere a fronteira orientada positivamente.
Passo 1
O exercício já dá a curva como fronteira de uma região, então vamos logo usar Green:
Ele também diz que a curva ta orientada positivamente, então não devemos ter nenhum problema pra aplicar o teorema. Só vamos, antes, entender nossa região.
Passo 2
A região é limitada por duas circunferências, as duas centradas na origem, uma de raio e outra de raio :
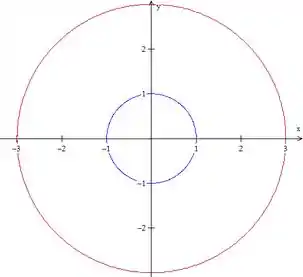
O que sugere coordenadas polares, só vamos ver como que fica os termos dentro da integral:
Bem, coordenadas polares é uma ótima ideia!
Passo 3
Vamos lembrar como que é:
E os limites vão ser simplesmente:
Então nossa integral vai ficar:
Pronto, sem mistério!
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 19-22, encontre o trabalho realizado por F sobre acurva na direção de t crescente F = 6 z i + y 2 j - 12 x k r ( t ) = ( s e n t ) i + ( c o s t ) j + ( t / 6 ) k , 0 ≤ t ≤ 2 π
Nos Exercícios 19-22, encontre o trabalho realizado por F sobre acurva na direção de t crescente F = z i + x j + y k r ( t ) = ( s e n t ) i + ( c o s t ) j + t k , 0 ≤ t ≤ 2 π
Como se calcula o trabalho realizado por uma força para mover uma partícula ao longo de uma curva? Dê um exemplo.
Use o Teorema de Green para achar o trabalho realizado pela força F x , y = x x + y i + x y 2 j ao mover uma partícula da origem ao longo do eixo x até( 1,0 ) , em seguida ao longo de um segmento de r
Nos Exercícios 19-22, encontre o trabalho realizado por F sobre a curva na direção de t crescente.