USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 2 - 2022.1, Questão 8c
Calcule
, sendo a fronteira da região limitada por , e , percorrida uma vez no sentido horário.
Passo 1
Olá meu amigo, tudo bem? Yuri aqui e vamos começar a resolução dessa querida atividade. Primeiro vamos dar uma olhada na região
Abaixo que é a região que iremos integrar.
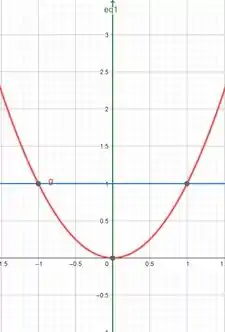
O caminho que iremos seguir é o caminho pela linha verde até e depois iremos seguir a linha azul até e depois iremos seguir até a origem por . Uma forma interessante de seguir esse caminho é montarmos uma integral para cada caminho explicitado e somar
Passo 2
Então para
Para
E agora para
Agora somando todos os resultados
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 19-22, encontre o trabalho realizado por F sobre acurva na direção de t crescente F = 6 z i + y 2 j - 12 x k r ( t ) = ( s e n t ) i + ( c o s t ) j + ( t / 6 ) k , 0 ≤ t ≤ 2 π
Nos Exercícios 19-22, encontre o trabalho realizado por F sobre acurva na direção de t crescente F = z i + x j + y k r ( t ) = ( s e n t ) i + ( c o s t ) j + t k , 0 ≤ t ≤ 2 π
Como se calcula o trabalho realizado por uma força para mover uma partícula ao longo de uma curva? Dê um exemplo.
Use o Teorema de Green para achar o trabalho realizado pela força F x , y = x x + y i + x y 2 j ao mover uma partícula da origem ao longo do eixo x até( 1,0 ) , em seguida ao longo de um segmento de r
Nos Exercícios 19-22, encontre o trabalho realizado por F sobre a curva na direção de t crescente.