(Adaptada) Uma superfície quente a deve ser resfriada fixando-se aletas de alumínio de de comprimento e de diâmetro. A temperatura ambiente é de e o coeficiente de transferência de calor nas superfícies é de .
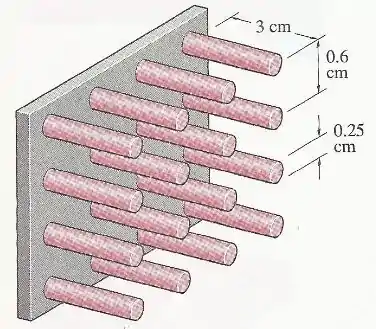
Determine a taxa de transferência de calor da superfície de cada aleta. Também determine a eficácia de cada aleta.
Passo 1
A taxa de transferência de calor da superfície da aleta é dada por:
Então precisamos começar calculando a sua eficiência . Olhando na tabela na Teoria desse tópico (e provavelmente no seu livro também). Vemos que:
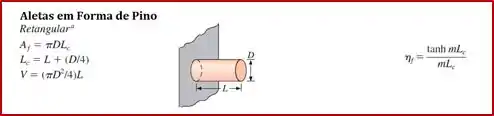
Sendo , onde:
Substituindo os valores:
Dessa forma, a eficiência da aleta será:
Passo 2
A área de troca da aleta é dada por:
Substituindo os valores:
Passo 3
Finalmente, a taxa de transferência de calor será:
Substituindo os valores:
Passo 4
A eficácia da aleta é dada por:
Em que é a área da seção transversal na base da aleta, logo:
Substituindo os valores: