Uma barra de diâmetro e condutividade térmica se projeta na direção normal, a partir de uma parede de uma fornalha que está a uma temperatura e é coberta com um isolamento de espessura . A barra é soldada à parede da fornalha e é utilizada como um gancho para suporte de cabos de instrumentação. Para evitar danos aos cabos, a temperatura da barra em sua superfície exposta () deve ser mantida abaixo do limite de operação especificado de . A temperatura do ar ambiente é é o coeficiente de convecção,.
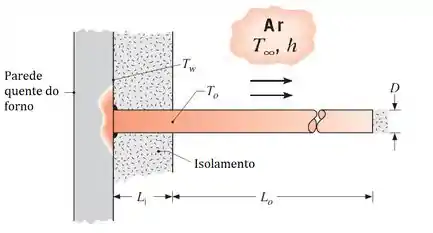
Calcule a temperatura da superfície exposta em função dos parâmetros térmicos e geométricos dados. A barra possui um comprimento exposto de e sua extremidade é bem isolada. Verifique se a temperatura ultrapassa o limite.
Passo 1
Antes de partir pros cálculos, bora entender a situação? No problema, a gente tem uma aleta de seção uniforme circular, em que parte dela está isolada e parte dela pode trocar calor. Além disso, sua extremidade também está isolada!
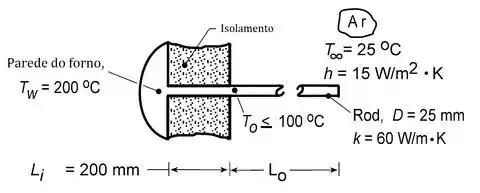
Como o forno é a região mais quente da situação, esperamos que o fluxo saia de sua parede em sentido do ar ambiente.
Mas, como a parte inicial da aleta está isolada, a energia é transportada somente por condução incialmente ao longo da aleta e, depois, ela passa a ser transportada por condução até o final, mas também é liberada por convecção para o ambiente na região sem isolamento. Entendido?

Bom, no problema, a temperatura de toda a barra não deve ultrapassar os . Mas se a gente garantir que a temperatura logo após o isolamento é menor que , então garantimos que toda a barra estará numa temperatura menor que .
Isso acontece porque ao longo da barra, ela troca calor com o ambiente e a temperatura vai diminuindo.
Passo 2
Beleza! Entendido o problema, a gente pode então usar nossa estratégia de montar o circuito térmico pra achar a temperatura :
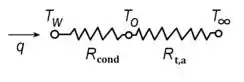
Como a taxa é constante ao longo de todo o circuito, a gente tem duas formas de se fazer a questão pelo menos:
I) Por meio das equações analíticas da taxa de calor de aletas
A gente sabe que a taxa de calor que passa por uma aleta de seção uniforme com extremidade adiabática (caso ) é dada por:
Em que:
Como a taxa é constante, a gente pode escrever que:
Substituindo a expressão de :
Nessa equação, a única incógnita é a temperatura e a gente consegue resolver!
Passo 3
A segunda forma de fazer a questão é:
II) Por meio dos gráficos de eficiência.
Se a taxa é constante, então a taxa de calor que passa pelo trecho isolado é igual à taxa que passa por todo o sistema:
Isolando a temperatura na equação, a gente fica com:
Em que as temperaturas e são conhecidas e as resistências são calculadas por:
E, assim, a gente pode calcular cada uma das resistências pra determinar a temperatura . Daí pra calcular a , a gente precisaria da eficiência (), que é obtida por um dos gráficos que vimos na teoria!
Passo 4
Aqui vou fazer com vocês a resolução pela equação analítica, que é sempre mais preciso usar equações do que gráficos! Recapitulando, a gente descobriu a seguinte equação:
Então, bora calcular o que dá pra calcular, como: o perímetro , o valor de e a resistência por condução .
O perímetro é dado por:
E o valor de é dado abaixo:
Em que a área é a área transversal da aleta, ou seja, a área de um círculo como diâmetro ! Sendo assim:
Agora, a gente pode calcular a resistência de condução:
Substituindo os valores:
Passo 5
Pronto! Substituindo todos os valores conhecidos, ficamos com:
Em que, o valor de será:
Dessa maneira, substituindo na equação:
Reorganizando a equação:
Isolando a temperatura:
Isso equivale a cerca de . Logo, a temperatura vai ultrapassar o limite estabelecido de .
Resposta
A temperatura equivale, em graus Celsius, a . Logo, a temperatura vai ultrapassar o limite estabelecido de .