Dois tubos de vapor de ferro fundido de de comprimento e de espessura com um diâmetro exterior de estão ligados um ao outro através de dois flanges de de espessura com um diâmetro exterior de .
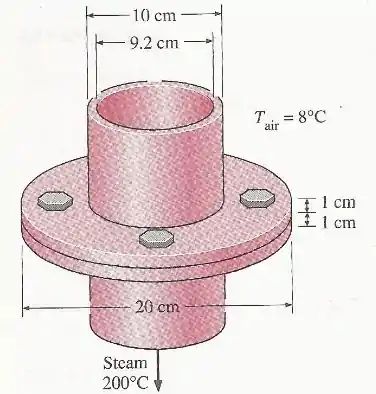
O vapor flui dentro do tubo a uma temperatura média de com um coeficiente de transferência de calor de . A superfície externa do tubo é exposta a um ambiente a , com um coeficiente de transferência de calor de .
Desconsiderando os flanges, determine a temperatura média da superfície externa do tubo.
Usando esta temperatura para a base do flange e tratando os flanges como as aletas, determine a eficiência da aleta e a taxa de transferência de calor dos flanges.
Qual comprimento de tubo é a seção de flange equivalente a para fins de transferência de calor?
Passo 1
Desconsiderando os flanges, determine a temperatura média da superfície externa do tubo.
O circuito térmico que representa o drama aqui é o seguinte:

Onde e são as resistências térmicas de convecção nas superfícies interna e externa respectivamente.
“Qual é a ideia aqui?!”
Podemos calcular a temperatura na superfície interna da seguinte forma:
Mas nós ainda não temos a taxa de transferência de calor . Mas podemos calculá-la utilizando a resistência térmica total do sistema:
Show de bola! Vamos fazer isso então!
Passo 2
Vamos começar pelas resistências térmicas, ok?
- Resistência térmica de convecção na superfície interna:
- Resistência térmica de condução:
- Resistência térmica de convecção na superfície externa:
Como estamos trabalhando com um cilindro, a resistência térmica de condução será:
Como temos três resistências térmicas em série, a resistência térmica total será:
Passo 3
Agora podemos calcular a taxa de transferência de calor no sistema:
Substituindo os valores:
Passo 4
Já podemos calcular a temperatura na superfície externa agora.
Passo 5
Usando esta temperatura para a base do flange e tratando os flanges como as aletas, determine a eficiência da aleta e a taxa de transferência de calor dos flanges.
A eficiência da aleta pode ser calculada através do gráfico abaixo:
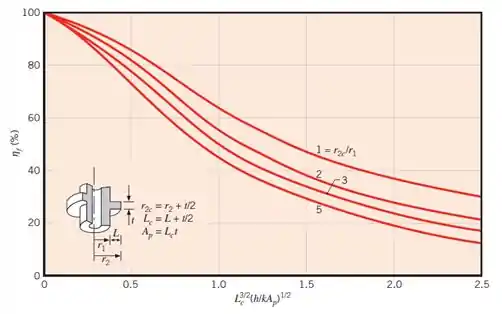
Para isso, precisamos dos seguintes valores:
Onde:
Substituindo todos os valores:
Utilizando esses dados no gráfico, encontraremos:
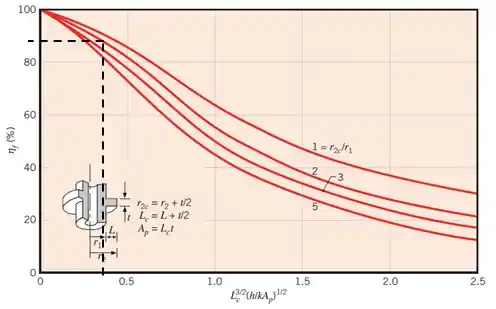
Passo 6
A taxa de transferência de calor através do flange será dada por:
Onde:
Logo, a taxa de transferência de calor será:
Passo 7
Qual comprimento de tubo é equivalente à seção de flange para fins de transferência de calor?
O tubo de 6 metros transfere calor a uma taxa de:
Logo, por metro, essa taxa de transferência de calor passa a ser:
Sabendo que o flange transfere calor a uma taxa de , o comprimento equivalente será:
Resposta