Dois tubos de ferro fundido são unidos por flanges de ferro fundido, conforme mostrado abaixo.

O diâmetro interno do tubo é e seu diâmetro externo é de . O diâmetro externo da união flangeada é , com espessura de . Dentro do tubo escoa vapor a , com coeficiente de transferência de calor de .
O tubo e a união flangeada perdem calor para o ar a com coeficiente de transferência de calor de . No regime permanente e considerando-se perfeito contato entre os flanges:
Calcule a temperatura da superfície externa do tubo, sem a união flangeada;
Com o valor da temperatura externa do tubo calculado no item anterior, calcule a taxa de calor perdida para o ar pela união flangeada.
Calcule o comprimento de tubo necessário para transferir a mesma taxa dissipada através da união flangeada.
Passo 1
Calcule a temperatura da superfície externa do tubo, sem a união flangeada;
O circuito térmico que representa esse sistema é dado por:
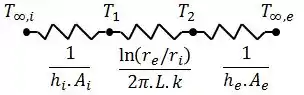
Nesse caso, estamos interessados em calcular a temperatura . Pra isso, vamos precisar da taxa de transferência de calor, que pode ser calculada utilizando-se as resistências térmicas.
Onde é a resistência térmica total do sistema, dada por:
Assim, a taxa de transferência de calor será:
Para calcular a temperatura , vamos comparar esse valor com a taxa de transferência de calor entre a superfície da tubulação e o ar externo. Logo:
![]()
Passo 2
Com o valor da temperatura externa do tubo calculado no item anterior, calcule a taxa de calor perdida para o ar pela união flangeada.
Como a flange se trata de uma superfície aletada, podemos calcular a transferência de calor utilizando a sua eficiência da seguinte forma:
Onde:
A eficiência da aleta é dada através de um gráfico, onde:
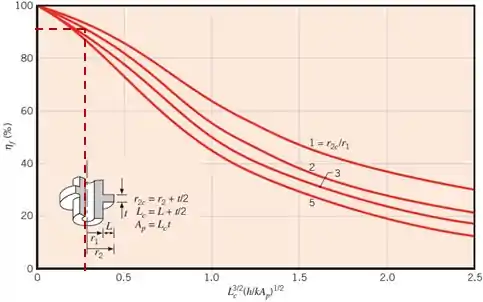
Dessa forma, a taxa de transferência de calor será:
![]()
Passo 3
Calcule o comprimento de tubo necessário para transferir a mesma taxa dissipada através da união flangeada.
Nós encontramos no Passo 1 que:
Substituindo o valor de que encontramos, teremos:
![]()
Resposta