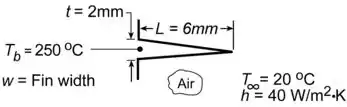
Aletas de alumínio () de perfil triangular são fixadas em uma parede cuja temperatura de superfície é . A base da aleta possui de espessura e seu comprimento é de . O sistema está no ar ambiente a temperatura de é o coeficiente de convecção de superfície é .
Quais são a eficiência e a efetividade da aleta?
Qual o calor dissipado por unidade de largura para uma única aleta?
Passo 1
Quais são a eficiência e a efetividade da aleta?
O enunciado propõe uma aleta triangular como mostrado aqui embaixo:
Para este tipo de geometria, a gente precisa tirar a eficiência no gráfico:
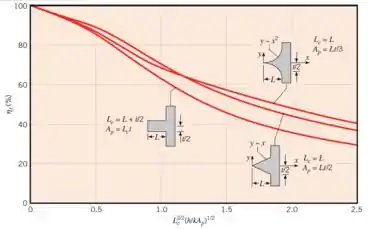
Pra isso, a gente precisa calcular o valor do eixo do gráfico ():
Em que:
Assim:
Pelo gráfico:
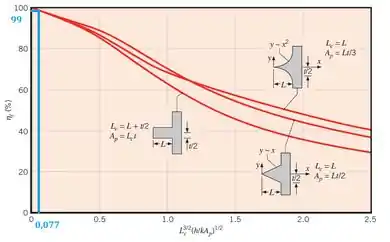
Logo:
Passo 2
Por definição, a efetividade e a eficiência de aletas são calculadas, respectivamente, por:
Então a gente pode relacionar as duas por meio da taxa :
Assim:
Passo 3
Vamos trabalhar nas áreas para calcular a efetividade da aleta. O termo é a área da aleta e é a área da seção transversal na base. Elas são dadas por:
Em que pode ser entendido pela imagem abaixo:
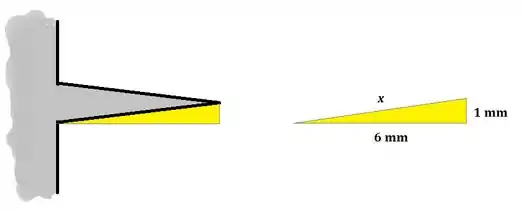
Logo:
Dividindo pela largura , a gente fica com a área por unidade de comprimento:
Além disso, a área da base por unidade de comprimento será:
Dessa maneira, a efetividade será:
Passo 4
Qual o calor dissipado por unidade de largura para uma única aleta?
A taxa de calor por unidade de largura pode ser calculada tanto pela eficiência quanto pela efetividade, dado que a gente já sabe as duas!
Vou escolher usar a efetividade, mas tanto faz, tá bem? :) Pela definição:
Logo:
Dividindo pela largura da aleta () em ambos os lados, ficamos com:
Substituindo os valores do enunciado:
Resposta