Suponha que você tenha uma escolha entre uma aleta retangular e uma aleta de perfil triangular construída de alumínio puro (propriedades à ), ambos com uma espessura na base de . A profundidade da aleta é de .
O coeficiente convectivo é de e a temperatura do meio é de enquanto a base da aleta está a .
A aleta retangular possui de altura e a aleta de perfil triangular possui de altura. Qual dessas terá a melhor relação (mais favorável em termos térmicos) de taxa de transferência de calor por peso de material para compor a aleta?
Passo 1
Antes de qualquer coisa, vamos buscar as propriedades do alumínio a . De acordo com a tabela A.1 do Incropera:
Agora podemos seguir em frente.
Passo 2
Vamos começar tratando da aleta retangular. Como a área transversal é constante na aleta, podemos usar as soluções tabeladas.
Como temos um caso onde há convecção na extremidade, a taxa de transferência de calor na aleta é dada por:
Onde:
Logo:
Finalmente:
![]()
Passo 3
O peso da aleta retangular é dada por:
Assim, para a aleta retangular, a relação e taxa de transferência de calor por peso de material é dada por:
![]()
Passo 4
Para a aleta triangular, não podemos usar uma equação tabelada porque a área de seção transversal não é constante. Então vamos calcular a taxa de transferência de calor usando a sua eficiência, dada por:
Para este tipo de geometria, a gente precisa tirar a eficiência no gráfico:
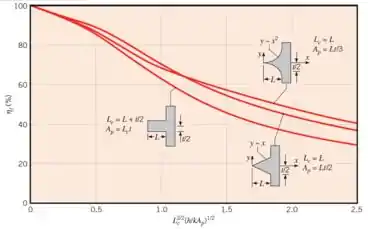
Pra isso, a gente precisa calcular o valor do eixo do gráfico ():
Em que:
Assim:
Pelo gráfico:
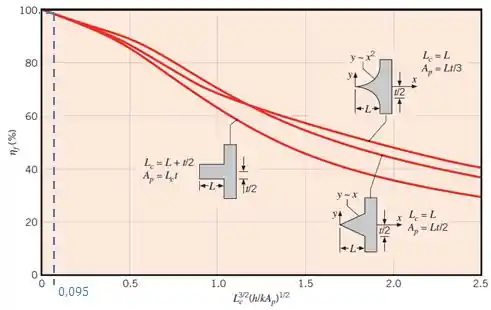
Passo 5
A área total de troca térmica da aleta triangular é dada por:
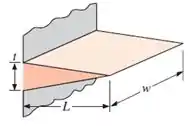
Assim, a taxa de transferência de calor será:
![]()
Passo 6
O peso da aleta triangular será:
Assim, para a aleta triangular, a relação de taxa de transferência de calor por peso de material é dada por:
![]()
Comparando as duas aletas, a aleta retangular apresenta uma melhor relação de taxa de transferência de calor por peso de material.
Resposta
Aleta retangular:
Aleta triangular: