Tubos de aço utilizados no transporte de água pressurizada são unidos por flanges de espessura . Os diâmetros interno e externo dos tubos são e , respectivamente, e o diâmetro externo dos flanges é .
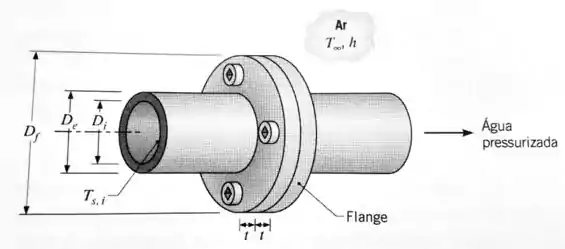
Em condições normais de operação, a superfície interna do tubo encontra-se a uma temperatura de , enquanto o ar ambiente está a . Se o coeficiente de convecção nas superfícies dos flanges é , qual a perda de calor através dos flanges? Considere a condutividade térmica do tubo e do flange iguais a.
Passo 1
Pra achar a taxa de calor que é perdida pelo sistema, bora dar uma olhadinha na vista lateral do desenho aqui embaixo:
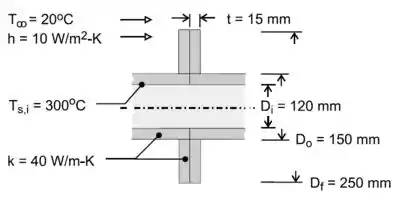
O que tá acontecendo nesse problema? A superfície mais interna do sistema está bem quente () e tem um fluido a temperatura ambiente do lado de fora (). Dessa forma, a gente espera que haja um fluxo de calor de dentro pra fora.
A presença dos flanges acaba tendo a função de uma aleta, pois aumenta a área de troca térmica para o ambiente externo. Então, é só a gente fazer usar as fórmulas de aletas! ^^
Já que não há geração em nenhum dos materiais, a gente pode usar a estratégia do circuito térmico! Ficaria da seguinte maneira:
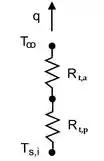
Então, a taxa de calor pode ser escrita em função das resistências:
Em que as resistências térmicas de condução na parede cilíndrica () e no flange () são calculadas por:
Passo 2
Bora calcular as resistências! Primeiro com a que a gente já tá mais acostumado:
- Resistência térmica de condução na parede cilíndrica:
- Resistência térmica de uma aleta anular simples (flange):
Substituindo os valores do enunciado:
Passo 3
Agora, vamos à resistência que mais interessa:
Da expressão aqui em cima, a gente só sabe o coeficiente , mas precisamos determinar a área () e eficiência da aleta ().
A área da aleta é essa área aqui em vermelho:
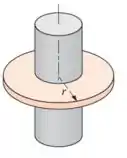
Então, a gente pode escrever que:
Mas a gente pode usar aquela estratégia do raio corrigido (), que é quando a gente assume que a contribuição da área lateral é adicionada à área do disco. Sendo assim:
Em que:
Substituindo os valores do enunciado:
Passo 3
Agora só falta a eficiência ()! Pra calcular a eficiência desse formato de aleta (anular), a gente tem que utilizar o gráfico que já vimos:
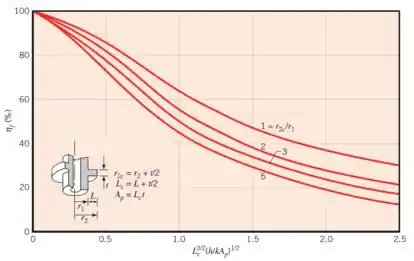
Para determinar a eficiência, a gente precisa então saber qual das quatro curvas representa a nossa aleta e calcular com o valor desse eixo aí loucão. Então, bora lá!
Bora calcular o valor de x do gráfico:
Em que e são calculados pelas expressões mostradas no gráfico:
Além disso:
Ufa! Agora a gente pode finalmente calcular o valor de x:
Pra saber qual das curvas serve pra gente, precisamos calcular a razão entre os raios:
Agora vamos voltar para o gráfico.
Passo 4
Não tem nenhuma curva com o valor que encontramos, mas a gente pode colocar mais ou menos entre as curvas de razão igual a e , um pouco mais próximo da curva de .
Agora a gente já pode marca no gráfico a posição da abscissa e ver a eficiência correspondente:
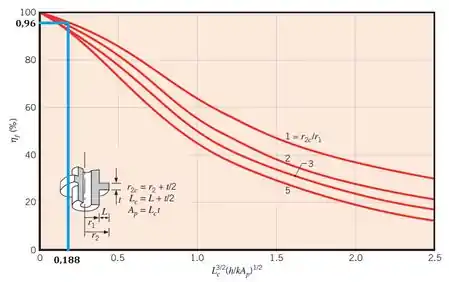
Concluimos, assim, que:
Passo 5
Com a área e eficiência calculadas, a gente pode finalmente determinar a resistência térmica da aleta:
Logo:
Passo 6
Prontinho! Agora ficou fácil calcular a taxa de calor: