![]()
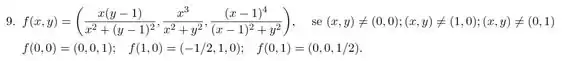
Passo 1
Bom, vemos que essa função tem definições diferentes nos pontos
e
e
e
Então parece uma boa testar a diferenciabilidade em cada um desses pontos.
Passo 2
Vamos começar pelo ponto :
E vamos primeiro testar a continuidade da função nesse ponto.
Para a função ser contínua, todas as suas funções componentes tem que ser contínuas nesse ponto. Começando pela primeira componente:
Para ela ser contínua,
Se fizermos a substituição, vamos chegar na indeterminação .
Se você observar, o grau do numerador é menor que o grau do denominador, então esse limite tá com a maior cara de que não existe.
Pra provar isso, vamos testar calcular o limite por caminhos diferentes e vê no que dá.
Primeiro pelo caminho e .
Agora pelo caminho e :
Opa, calculando o limite por dois caminhos diferentes, eles deram valores diferentes, ou seja, esse limite realmente não existe.
Assim, como já na primeira componente vimos que ela não é contínua em , então nossa função vetorial não é continua nesse ponto.
Se ela não é sequer continua, então ela também não pode ser diferenciável em .
Passo 3
Beleza, agora vamos para o ponto
Mas, antes de tudo, vamos calcular a derivada da nossa função:
Então
Substituindo no limite:
Como o limite deu zero, é diferenciável em .
Passo 4
Beleza, agora vamos para o ponto
A derivada da nossa função é:
Para
Então
Substituindo no limite:
E esse limite não existe. Sendo assim, a função não é diferenciável em .
Passo 5
Para todos os outros pontos que não são esses que a gente já calculou, repara uma coisa.
A matriz das derivadas é
E todas as funções componentes são funções racionais. E funções racionais são de classe no seu domínio.
Repare que os pontos problemáticos seriam justamente aqueles que a gente já testou nos passos anteriores. Então para todos os outros pontos, podemos dizer que a função é diferenciável, pois ela é de classe .
Resposta
Ei, a resposta está no passo a passo :)