![]()
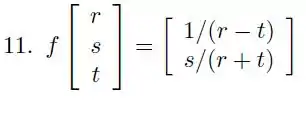
Passo 1
Vamos começar calculando as derivadas da nossa função num ponto qualquer
Passo 2
Agora observa uma coisa:
As funções que compõe essa matriz de derivadas ou são funções constantes, ou são funções compostas por polinômios (nesse caso, são racionais).
E funções racionais são funções de classe no seu domínio.
E o domínio é:
Então, como ser de classe é condição suficiente para ser diferenciável, temos que essa função é diferenciável em todos os pontos de seu domínio.
Assim, ela não é diferenciável somente quando e .
Resposta
Ei, a resposta está no passo a passo :)