Deseja-se difundir o metal A numa barra de metal B a partir de um filme de A depositado em uma face da barra de B, conforme indicado na figura abaixo. Após um tratamento a por , a concentração A a uma distância de a partir da interface é de . Qual deveria ser a temperatura para que a mesma concentração ( A) fosse atingida em uma posição de a partir da interface, supondo o mesmo tempo de tratamento? Considerar as hipóteses e condições de contorno apresentadas abaixo.
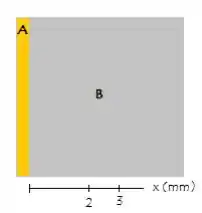
Hipóteses e condições de contorno:
- A concentração inicial de A em B é igual a é constante ao longo do corpo B.
- Nenhum átomo de B atinge a extremidade da barra de metal B oposta à face que recebeu o depósito de metal A, ou seja, a concentração de A nessa extremidade da barra de B é igual a durante todo o tratamento térmico de difusão.
- A concentração de A na interface AB é mantida constante durante todo o tempo de tratamento térmico de difusão e é igual a .
- A difusão de B em A pode ser considerada desprezível nas condições de tratamento térmico.
Equações:
- Utilizar a seguinte solução para a 2ª Lei de Fick para difusão não estacionária:
- A equação para o coeficiente de difusão é a seguinte:
Dados:
Passo 1
Opa! Fala aí! Essa parece cabeluda, né? Relaxa que nós damos conta juntos!
Olha só, o enunciado nos mostra duas situações diferentes, temos a parte do tratamento 1 e do tratamento 2, vamos anotar nossos dados para cada um deles:
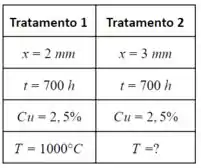
Beleza! Agora usando as condições de contorno que foram dadas, onde e são constantes, isso quer dizer que todo o lado esquerdo da função é constante:
constante
Sendo assim, temos que:
constante
E mesmo sofrendo tratamentos diferentes, essa constante nos dois tratamentos serão iguais! Logo podemos dizer que:
Passo 2
Se as funções são iguais, então o que está dentro delas também é:
Opa! Se os tempos são iguais, então temos que:
O coeficiente do tratamento 1, podemos encontrar pois temos todos os dados, certo?
Para o tratamento 2 não podemos fazer isso! Porque não temos a temperatura, que é justamente o que estamos procurando, ok? Mas relaxa! Agora vamos voltar na relação que fizemos ali em cima e vamos conseguir achá-la!
Vamos ter então que:
Passo 3
E agora pra achar a temperatura? Como vamos fazer?
Opa! Podemos usar a relação do próprio coeficiente de difusão! Se liga só:
Temos então que:
Rearranjando vamos ter:
E tirando o dos dois lados, temos:
Sendo assim, a temperatura no tratamento 2, será:
ou
Prontinho! Demos conta de tudo!