Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Difusão em Regime Transiente

Ver Teoria
Exercício 11123456789101213

Enunciado

Determinar o tempo de carburação necessário para ancorar uma concentração de carbono de 0,45   w t % em uma posição de 2   m m em uma liga de ferro-carbono que contenha inicialmente 0,20   w t % . A concentração da superfície deve ser mantida em 1,30   w t % e o tratamento deve ser conduzido em 1000   ° C .

Dados: D 0 = 2,30 ⋅ 10 - 5   m 2 / s , Q d = 148000   J / m o l , R = 8,31   J / m o l

Passo 1

Partiu resolver mais uma! Estamos indo bem! O enunciado quer que a gente encontre o tempo de carburação nas condições dadas… Vamos começar anotando nossos dados, ok?

  • C S = 1,30   w t %
  • C o = 0,20   w t %
  • C x = 0,45   w t %
  • x = 2   m m → 2 ⋅ 10 - 3   m
  • T = 1000 ° C → 1273   K

Bom, vamos usar a equação que relaciona os nossos dados com o que queremos… Essa equação é a segunda Lei de Fick:

C S   -   C x C S   -   C o = e r f x 2 D t

Opa! De cara a gente tá vendo que tá faltando o coeficiente de difusão pra gente achar o tempo, né? Vamos achar ele com a seguinte equação:

D = D 0 ⋅ e - Q d R ⋅ T

Substituindo os dados do enunciado:

D = 2,30 ⋅ 10 - 5 ⋅ e - 148000 8,31 ⋅ 1273

Então o coeficiente de difusão será:

D = 1,9308 ⋅ 10 - 11   m 2 / s

Agora sim vamos para a 2ª Lei de Fick!

Passo 2

Substituindo apenas o lado esquerdo na equação, vamos ter:

1,3   -   0,45 1,3   -   0,2 = e r f x 2 D t

Vamos ficar com:

0,7727 = e r f x 2 D t

Agora vamos usar essa tabelinha aqui pra achar o valor de z e descobrir o tempo que estamos procurando:

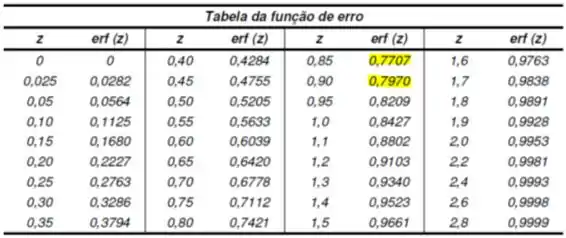
Eita! Olha só nosso valor de e r f não está na tabela… Precisamos interpolar! Vamos nessa:

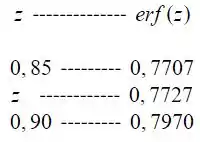
Vamos ter então:

z - 0,85 0,90 - 0,85 = 0,7727 - 0,7707 0,7970 - 0,7707

Ficamos com:

z = 0,8538

Isso quer dizer:

x 2 D t = 0,8538

Substituindo nossos dados:

2 ⋅ 10 - 3 2 1,9308 ⋅ 10 - 11 ⋅ t = 0,8538

Rearranjando, ficaremos com:

t = 10 - 6 1,9308 ⋅ 10 - 11 ⋅ 0,8538 2

O tempo que buscamos é:

t = 71048   s

ou

t ≈ 19,7   h

Uhull!! Arrasamos!

Resposta

t ≈ 19,7   h

Exercícios de Livros Relacionados

5. Calcule o valor do coeficiente de difusão da amônia em nitrogênio a 0 ° C , considerando:a) a amônia sem polaridade;b) admita a polaridade da amônia.
Uma fibra ótica de sílica vítrea com 100 μm de diâmetro é usada para enviar sinais óticos de um sensor localizado no interior de uma câmara de hidrogênio. O hidrogênio está a uma pressão de 20 bar. A
Se uma quantidade de energia Q " 0 J m 2 for liberada instantaneamente, por exemplo, a partir de um laser pulsante, e ela for absorvida pela superfície de um meio semi-infinito, sem perdas concomitant
Uma folha quadrada (100 mm x 100 mm) de um polímero, com espessura de 1 mm, está suspensa em uma balança de precisão no interior de uma câmara caracterizada por uma temperatura e umidade relativa de T
Aço é carburizado em um processo a alta temperatura que depende da transferência de carbono por difusão. O valor do coeficiente de difusão depende fortemente da temperatura e pode ser aproximado pela