Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Difusão em Regime Transiente

Ver Teoria
Exercício 51234678910111213

Enunciado

Um teste de incêndio é conduzido sobre uma grande massa de concreto inicialmente a uma temperatura de 15 ° C . A temperatura da superfície atinge 500 ° C instantaneamente. Estime o tempo requerido para que a temperatura a uma profundidade de 30   c m atinja 100 ° C . O concreto pode ser considerado como um sólido semi-infinito.

Dados: k = 1,4   W / m ° C , ρ = 2300   k g / m ³ , C = 880   J / k g ° C , α = 6,9 ⋅ 10 - 7   m ² / s

Passo 1

Fala aí! Vamos resolver essa questãozinha juntos! Bom, o enunciado já nos deu o bizu! Ele diz que o concreto pode ser considerado um sólido semi-infinito, então pra gente encontrar o tempo podemos usar a equação:

T x ,   t   -   T 1 T 0   -   T 1 = e r f x 2 α ⋅ t

Substituindo nossos dados na esquerda da equação, temos:

100   -   500 15   -   500 = e r f x 2 α ⋅ t

Logo, nossa função erro tem que ser igual a:

e r f x 2 α ⋅ t = 0,8347

Para saber quem é o termo z , que fica dentro da função erro, vamos usar a seguinte tabela:

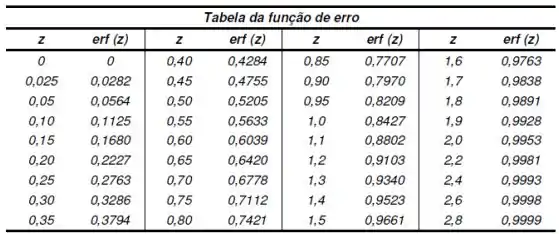
Nosso resultado não está aí, então vamos encontrar dois valores que nos permitam fazer uma interpolação.

Passo 2

Pegando um valor acima e um valor abaixo do que precisamos, vamos ter:

z →   e r f z

0,95 → 0,8209

z → 0,8347

1,0 → 0,8427

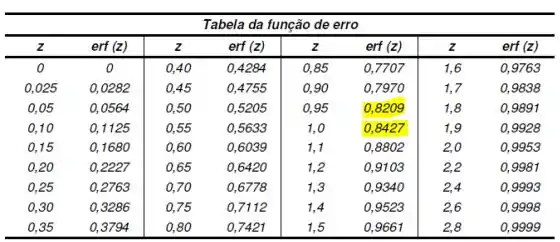
Interpolando vamos ter que:

z - 0,95 1,0 - 0,95 = 0,8347 - 0,8209 0,8427 - 0,8209

Teremos então:

z = 0,9816

Opa! Então isso quer dizer que:

x 2 α ⋅ t = 0,9816

Substituindo nossos dados:

0,3 2 6,9 ⋅ 10 - 7 ⋅ t = 0,9816

Rearrumando, ficamos com:

t = 0,09 4 ⋅ 6,9 ⋅ 10 - 7 ⋅ 0,9635

Temos então que:

t = 33844   s

ou

t = 9,4   h

Prontinho!!

Resposta

t = 9,4   h

Exercícios de Livros Relacionados

5. Calcule o valor do coeficiente de difusão da amônia em nitrogênio a 0 ° C , considerando:a) a amônia sem polaridade;b) admita a polaridade da amônia.
Uma fibra ótica de sílica vítrea com 100 μm de diâmetro é usada para enviar sinais óticos de um sensor localizado no interior de uma câmara de hidrogênio. O hidrogênio está a uma pressão de 20 bar. A
Se uma quantidade de energia Q " 0 J m 2 for liberada instantaneamente, por exemplo, a partir de um laser pulsante, e ela for absorvida pela superfície de um meio semi-infinito, sem perdas concomitant
Uma folha quadrada (100 mm x 100 mm) de um polímero, com espessura de 1 mm, está suspensa em uma balança de precisão no interior de uma câmara caracterizada por uma temperatura e umidade relativa de T
Aço é carburizado em um processo a alta temperatura que depende da transferência de carbono por difusão. O valor do coeficiente de difusão depende fortemente da temperatura e pode ser aproximado pela