UFRJ – Física 3 2020.2 – P1 – Questão 33
(Uma observação: realmente existem respostas repetidas... Isso foi um erro de prova, beleza?)
Escolha uma:
- Força: ; Torque: ; o movimento será uma composição de uma translação para a esquerda com uma rotação em sentido horário.
- Força: ; Torque: ; o movimento será uma composição de uma translação para a esquerda com uma rotação em sentido horário.
- Força: ; Torque: ; o movimento será uma composição de uma translação para a direita com uma rotação em sentido horário.
- Força: ; Torque: ; o movimento será uma composição de uma translação para cima com uma rotação em sentido anti-horário.
- Força: ; Torque: ; o movimento será uma composição de uma translação para a esquerda com uma rotação em sentido horário.
- Força: ; Torque: ; o movimento será uma composição de uma translação para baixo com uma rotação em sentido anti-horário.
Passo 1
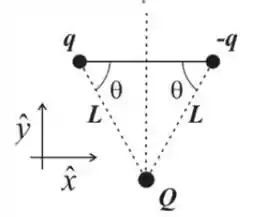
Fala galera, tudo bem? Essa questão parece complicada, mas não é, saca só! A ideia aqui é desenhar as forças que agem sobre as partículas desse dipolo e analisar quais componentes se anulam e quais se somam, resultando no movimento final.
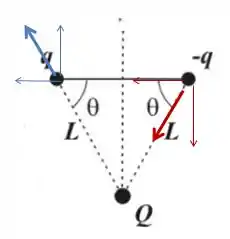Então segue o esquema das forças:
Aqui a gente vê que a rotação será em sentido horário. E quanto à translação? As forças estão representadas nas partículas do dipolo (vetores de linhas mais grossas, em vermelho e em azul). As componentes verticais das forças não resultarão em translação, mas as componentes horizontais sim, pois se somam. Elas apontam para a esquerda (são os vetores mais finos, representados em vermelho e azul no desenho).
Então teremos uma composição: rotação em sentido horário e translação para a esquerda.
Vamos calcular o módulo da força e do torque?
Passo 2
Primeiro a força: como cada carga do dipolo possui em módulo o mesmo valor, a força resultante vai ser duas vezes a força entre um par . A componente que nos interessa é a horizontal, então:
E a força entre duas cargas é:
Assim a força resultante é:
E a direção? Já sabemos que é horizontal para a esquerda, então em notação vetorial a força resultante é:
Passo 3
E por fim o torque!
Aqui embaixo vou fazer um esquema da componente da força que vai realizar torque (componentes verticais) com os vetores braço de alavanca (que unem cada carga ao centro do dipolo – vetor em verde):
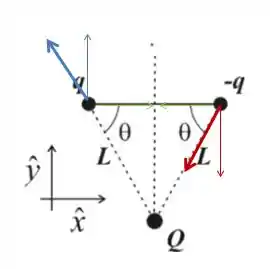
Note que nas duas cargas, usando a regra da mão direita, o torque é na direção . Então podemos somar as duas contribuições (você nem precisaria observar isso, vai sair naturalmente nas contas daqui a pouco).
O ângulo entre a força e o deslocamento é . O braço de alavanca é .
Daí o torque sobre uma das cargas é:
E o torque resultante vai ser a soma dos dois:
A força é , então:
E a direção? Pela regra da mão direita vimos que é , mas podemos confirmar matematicamente.
Olhando a carga , vetor força é na direção e o vetor braço de alavanca é na direção e a direção do torque vai ser dado pelo produto vetorial:
Agora olhando pra carga : o vetor força tem direção e braço de alavanca , assim o produto escalar entre eles fica assim:
Viu só? Os dois vetores apontam na mesma direção, então fez todo sentido a gente somar os torques lá no começo desse passo.
Passo 4
Agora vamos recapitular os resultados:
O torque:
A força:
O movimento: translação para esquerda e rotação no sentido horário.
Beleza?
E analisando as alternativas, a correta é a (a).
Espero ter ajudado!