Uma partícula com carga deve ser trazida de longe para um ponto próximo a um dipolo elétrico. Nenhum trabalho é feito se a posição final da partícula estiver sobre:
(a) a linha através das cargas do dipolo.
(b) uma linha que faz um ângulo de com o momento dipolar.
(c) uma linha que faz um ângulo de com o momento dipolar.
(d) uma linha perpendicular e que passa pelo centro do momento de dipolo.
(e) nenhuma das alternativas acima.
Passo 1
Primeiramente, vamos relembrar o que é um dipolo elétrico.
Um dipolo elétrico é um sistema formado por duas cargas pontuais de mesmo módulo e sinais contrários separados por uma distância . Veja a figura abaixo.

O ponto é o centro do dipolo. O vetor localiza o ponto onde está sendo calculado o potencial .
O potencial gerado por este dipolo segue o princípio da superposição, isto é, o potencial resultante é igual a soma dos potenciais gerados por cada carga. Matematicamente,
com a constante eletrostática.
Agora, vamos relembrar a definição de trabalho.
O trabalho do dipolo sobre um carga pontual pode ser calculado a partir da seguinte equação
sendo e o potencial gerado pelo dipolo sobre a carga nas posições inicial e final da trajetória, respectivamente.
Assim, no próximo passo, vamos analisar as condições para que . Simbora!
Passo 2
O potencial gerado pelo dipolo sobre a posição inicial da carga é dado por
sendo e os vetores que vão das cargas e , respectivamente, até a posição inicial da carga .
O enunciado diz que, inicialmente, a carga está muito afastada do dipolo elétrico. Assim, podemos dizer que a posição inicial da carga é tal que
Desta forma, utilizando a expressão para o potencial do dipolo, temos que
isto é, o potencial gerado pelo dipolo a uma distância muito grande do mesmo é nulo.
Portanto, a expressão para o trabalho do dipolo sobre a carga fica
Deste modo, para que , devemos ter necessariamente .
Assim, precisamos achar algum ponto em torno do dipolo em que o potencial seja nulo.
Veremos isso no próximo passo.
Passo 3
Vamos tentar entender sobre a posição final da carga .
No passo 1, vimos que o potencial gerado pelo dipolo é dado por
No passo 2, concluímos que para , então , isto é, o potencial gerado pelo dipolo sobre a carga na posição final do mesmo deve ser nulo.
Desta forma, temos que
isto é, a posição final da carga tem que ser tal que .
Analisando a primeira figura, vemos que isso ocorre quando as cargas e ponto final da trajetória formam um triângulo isósceles, com os vetores e de mesmo tamanho. Veja a figura abaixo.
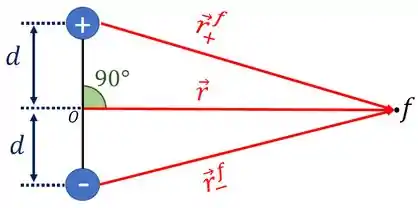
Assim, pela figura anterior, temos que quando o vetor faz um ângulo de com o dipolo elétrico.
Concluímos então que o potencial é nulo em qualquer ponto da linha que passa pelo centro do dipolo e faz um ângulo de com o dipolo.
Portanto, analisando as alternativas, vemos que a alternativa correta é a letra .