Quadrupolo elétrico.
A figura abaixo mostra um quadrupolo elétrico.
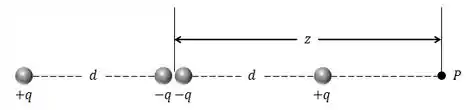
Ele é formado por dois dipolos com momentos de dipolo que são iguais em módulo, têm a mesma direção, mas sentidos contrários.
Mostre que o valor de sobre o eixo do quadrupolo, para um ponto a uma distância do seu centro (suponha que ) é dado por:
Onde é chamado de momento quadrupolar da distribuição de cargas.
Passo 1
Vamos nessa! Notou que esse desenho é meio diferente do que a gente tava vendo nesse capítulo? Isso porque não tem nenhum triângulo nesse desenho!
E agora? Qual é o campo elétrico de um dipolo gerado nesse caso?
Acompanha comigo. Olha o desenho abaixo:
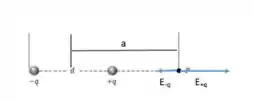
O campo resultante em P mede:
Simplificando, temos:
Considerando , . Logo, temos:
Além disso, dessa vez o campo elétrico tem o mesmo sentido do dipolo. Logo, a fórmula do campo elétrico gerado por um dipolo nesse caso é:
Onde é o módulo de uma das cargas, é a distância entre as cargas e é a distância entre o ponto médio entre as cargas e o ponto que estamos calculando o campo elétrico.
O momento dipolar elétrico é o vetor que aponta da carga negativa para a carga positiva.
Show de bola! O quadrupolo magnético nada mais é do que um arranjo com dois dipolos elétricos, então, o campo elétrico resultando do quadrupolo é o somatório do campo elétrico dos dois dipolos elétricos.
Passo 2
Vamos começar calculando o campo elétrico para o dipolo elétrico mais próximo do ponto .
Vou adotar o referencial positivo da esquerda para a direita, beleza?
Pra esse dipolo, a distância entre o centro do dipolo até o ponto é .
Sabemos que o sentido do campo é o mesmo do momento dipolo elétrico (que aponta da carga negativa para a positiva). Como o momento dipolar elétrico está apontando no sentido positivo do eixo , o campo elétrico para esse dipolo é dado por
Passo 3
Agora vamos calcular o campo elétrico para o dipolo mais longe do ponto .
Pra esse dipolo, a distância entre o centro do dipolo até o ponto é .
Como momento dipolar elétrico está apontando no sentido negativo do eixo , o campo elétrico para esse dipolo é dado por:
Passo 4
Por último, agora é só somar os dois e ver qual o campo elétrico resultante:
Tá beleza! Tudo o que fizermos aqui está certo! Então o problema em si acaba aqui... agora é só aquela parte chata de arrumar a equação até ficar igual ao que queremos.
Então agora é na base da disposição!
Vamos começar colocando o que os dois tiverem em comum em evidência, podemos?
Bora colocar aquele do denominador em evidência mas, pra fazer isso, quando tirarmos ele dos parênteses, vamos ter que elevar ele ao cubo.
Agora é o momento em que você precisa ter fé!
Então fica esperto pro que vamos fazer aqui porque é o único jeito de chegar na fórmula que precisamos...
O que vamos fazer aqui é aplicar a Série de Taylor... vou colocar isso em um próximo passo pra fazer um apelo dramático.
Passo 5
O que é a Série de Taylor? Onde vive? Como se alimenta?
Essas e outras perguntas, responderemos aqui!
A Série de Taylor é uma expansão de uma determinada função em torno de um certo ponto. Beleza, mas como assim?
Então, como, de acordo com o enunciado , você concorda que vai girar em torno de zero, se compararmos com ?
É esse o intuito da Série de Taylor, analisar uma função quando ela estiver próximo de um determinado ponto.
A expansão em Série de Taylor de uma determinada função em torno do ponto é dada por:
Beleza?!
Usando a Série de Taylor nas funções e em torno de , teremos o seguinte:
Agora é só arrumar essa bagaça! ;)
Onde a , logo:
Resposta
Ei, a resposta está no passo a passo :)