A figura abaixo mostra um dipolo elétrico. Determina (a) o módulo e (b) a orientação (em relação ao semi-eixo positivo) do campo elétrico produzido pelo dipolo em um ponto situado a uma distância .
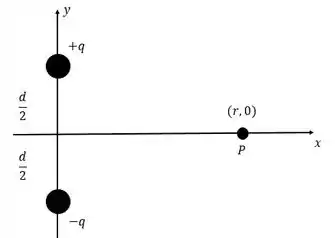
Passo 1
Calcular em função das variáveis o momento dipolo elétrico :
Passo 2
Exprimir o campo em função do dipolo:
Passo 3
Se apontarmos os dois campos produzidos pelas duas partículas vamos ter
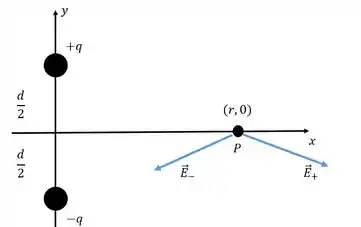
E ao somarmos vetorialmente teremos
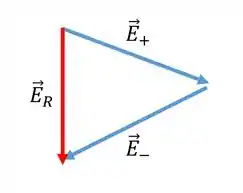
Logo o nosso campo elétrico aponta para baixo! Assim
Resposta
Logo, o campo elétrico vale:
Ele aponta para baixo e possui módulo igual a:
Exercícios de Livros Relacionados
Duas partículas com a mesma carga positiva q são mantidas fixas no eixo y, uma em y =d e a outra em y = - d. (a) Escreva uma expressão para o módulo E do campo elétrico em pontos do eixo x dados por x
Três cargas se situam nos vértices de um triângulo isósceles, como indica a figura 21.43. As cargas de ± 5μ C formam um dipolo.(a) Determine a força (módulo, direção e sentido) que a carga - 10μ C exe
Um dipolo elétrico é submetido a um campo elétrico uniforme E → de módulo 40N/C. A Fig. 22-58 mostra o módulo τ do torque exercido sobre o dipolo em função do ângulo θ entre o campo E → e o momento di
Uma molécula tem um dipolo dado por p → . A molécula está momentaneamente em repouso com p → fazendo um ângulo θ com um campo elétrico uniforme E → . Descreve o movimento subsequente do momento de dip
Um dipolo elétrico que tem momento de dipolo p → está localizado a uma distância perpendicular R de uma linha infinitamente longa de cargas que tem densidade linear uniforme λ . Considere que o moment