A molécula de água como um todo é eletricamente neutra, porém suas ligações químicas no interior da molécula de água produzem um deslocamente de cargas e o resultado disso é uma carga líquida negativa na extremidade ocupada pelo oxigênio e uma carga líquida na extremidade ocupada pelos hidrogênios, como mostra a Figura a) abaixo. Por isso, molécula assemelha a um dipolo elétrico .

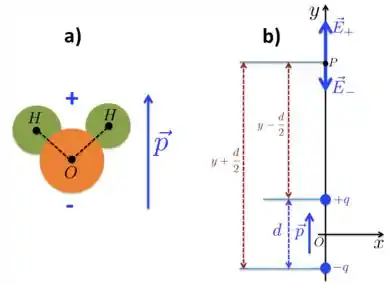
Dada essa situação, suponha agora que o dipolo elétrico da água seja e que ele esteja localizado na origem com o momento de dipolo   apontando no sentido , como mostrado na Figura b) acima. Um íon de cloro (), com carga igual a , está localizado no ponto . Supondo que seja muito maior do que a distância entre as cargas do dipolo elétrico:

1. Determine o módulo, a direção e o sentido da força que a molécula de água exerce sobre o íon de cloro ;
2. A força entre   e a carga é de atração ou repulsão?

a) Neste exercício, a gente precisa calcular o campo elétrico resultante , no ponto da Figura b) acima, produzido pelo par de cargas pontuais fixas e e depois tomar o limite para o obter o valor desse campo resultante quando tem uma distância . Blz? Vamos lá?

Bom, o módulo do campo elétrico produzido pela carga positiva em é:

e pela carga negativa é

O campo elétrico resultante vai estar na direção do eixo e tem módulo dado por

Tranquilo? O módulo do campo resultante é a diferença entre os módulos: . Agora, como , o vetor   estará apontanto na direção do eixo .

Portanto,