Duas partículas de cargas e são posicionadas sobre o eixo de um sistema de coordenadas, de forma que elas se encontram em e (), respectivamente. Considere um ponto sobre o eixo , a uma distância da origem. Se este ponto está muito distante da origem, de forma que , podemos afirmar que o campo elétrico produzido pelas partículas neste ponto tem intensidade proporcional a:
Passo 1
Pra gente matar essa questão, vamos colocar o que o enunciado diz na figura abaixo. O campo elétrico gerado pela carga positiva é de afastamento e está ao longo da reta . Já o campo , devido à , se aproxima desta carga e está o longo do segmento de reta . O campo resultante que vamos encontrar é aquele devido a um dipolo elétrico, que é exatamente o que temos aqui.
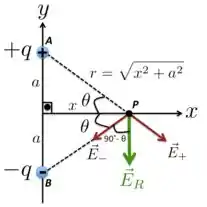
Como essas duas cargas têm o mesmo módulo e estão à mesma distância do ponto , as componentes dos campos e na direção do eixo tem a mesma direção, o mesmo módulo, mas sentidos opostos e por isso se cancelam. Basta, então, olharmos para as componentes desses campos na direção . Quando a gente somar essas componentes em vamos ter o campo elétrico resultante no ponto , que vai estar apontando na direção e sentido de .
Passo 2
O campo resultante no ponto será
em que o módulo é dado por
e, do triângulo retângulo da figura, tiramos que
Juntando tudo na expressão para o campo resultante no ponto :
Quando fazemos , podemos simplificar a expressão acima para
mostrando que, nesse limite, o campo elétrico resultante será proporcional a , que é como o campo elétrico produzido por um dipolo elétrico se comporta para distâncias muito grandes.
Resposta
Letra b.