Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Dipolos Elétricos

Ver Teoria
Exercício 27123456789101112131415161718192021222324252628293031

Enunciado

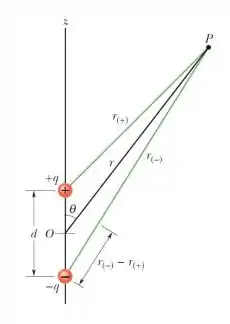
Um dipolo elétrico está localizado ao longo do eixo z como mostra a figura abaixo. A magnitude do momento de dipolo elétrico é definida como p = q d =   q d k , onde k é um versor unitário no sentido +   z . (a.1) (1,0 ponto) Determine o potencial elétrico do dipolo num ponto P qualquer, situado a uma distância r ( + ) da carga positiva e a uma distância r ( - )   da carga negativa. (a.2) (1,0 ponto) Obtenha a expressão para potencial elétrico do dipolo para pontos muito afastados do dipolo ( r   > >   d ). (b) (0,5 ponto) Utilize o resultado do item a.2 e calcule o campo elétrico produzido pelo dipolo a uma distância r do dipolo quando r > >   d .

Passo 1

L e t r a   A :

Bem... Sabemos que o campo o potencial elétrico de uma carga pontual qualquer q em um ponto qualquer P a uma distância r pode ser dado por...

V = 1 4 π ε 0 q r

O de duas cargas pontuais então será...

V = 1 4 π ε 0 q 1 r 1 + 1 4 π ε 0 q 2 r 2

No nosso caso, substituindo as cargas e as distâncias r delas do ponto P qualquer...

V = 1 4 π ε 0 + q r + + 1 4 π ε 0 - q r -

V = q 4 π ε 0 1 r + - 1 r -

Passo 2

L e t r a   B :

Veja bem... Queremos agora determinar uma expressão de V para pontos P muito longes de modo que r ≫ d ...

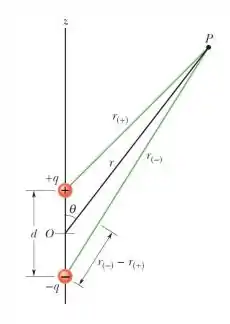
Então, a primeira tarefa será relacionar r e d . Depois a gente tenta simplificar o que a gente encontrar. Bora?

Passo 3

POW! Não sei se você consegue ver, mas existem dois triângulos ali...

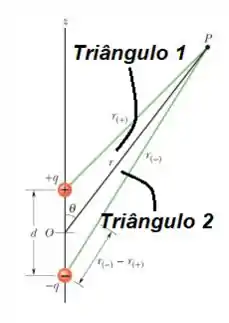
E pelas leis dos cossenos, podemos dizer que para r + ...

r + = r 2 + d 2 2 - 2 r d 2 cos ⁡ θ   →

r + = r 2 + d 2 2 - r d cos ⁡ θ  

E para r - , olhando agora para o triângulo 2, vamos ter algo semelhante! A diferença é de que o ângulo entre r e d / 2 é 180 ° - θ :

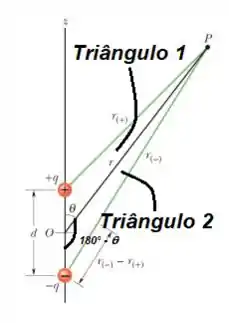
Então, pela Lei dos cossenos...

r - = r 2 + d 2 2 - r d cos ⁡ 180 - θ  

Como cos ⁡ 180 - θ = - cos ⁡ θ ...

r - = r 2 + d 2 2 + r d cos ⁡ θ

Passo 4

BELEZINHA! Então encontramos uma forma de escrever V apenas com relação a r e d e θ ...

V = q 4 π ε 0 1 r + - 1 r -   →

V = q 4 π ε 0 1 r 2 + d 2 4 - r d cos ⁡ θ - 1 r 2 + d 2 4 + r d cos ⁡ θ   →

Vamos começar agora a simplificação já que a gente sabe pelo enunciado ser o r ≫ d .

A primeira coisa que podemos fazer aqui é escrever essas raízes de outra forma...

V = q 4 π ε 0 1 r 2 + d 2 4 - r d cos ⁡ θ 1 / 2 - 1 r 2 + d 2 4 + r d cos ⁡ θ 1 / 2   →

V = q 4 π ε 0 r 2 + d 2 4 - r d cos ⁡ θ - 1 / 2 - r 2 + d 2 4 + r d cos ⁡ θ - 1 / 2   →

Belezinha! Agora veja... r ≫ d então é interessante meio que colocar r 2 em evidencia, veja:

V = q 4 π ε 0 r 2 - 1 / 2 r 2 r 2 + d 2 4 r 2 - r d r 2 cos ⁡ θ - 1 / 2 - r 2 - 1 / 2 r 2 r 2 + d 2 4 r 2 + r d r 2 cos ⁡ θ - 1 / 2   →

V = q 4 π ε 0 1 r 1 + d 2 4 r 2 - d r cos ⁡ θ - 1 / 2 - 1 r 1 + d 2 4 r 2 + d r cos ⁡ θ - 1 / 2   →

E porque que isso é legal? Porque aqui a gente começa a nossa primeira simplificação do dia: sabemos que r ≫ d , logo d 2 / r 2 é extremamente pequeno, afinal r já é muito grande imagina então r 2 ? Então, se essa expressão é muito pequena podemos desconsidera-la! Veja:

V = q 4 π ε 0 1 r 1 - d r cos ⁡ θ - 1 / 2 - 1 r 1 + d r cos ⁡ θ - 1 / 2   →

“Ah! Mas porque a gente não pode eliminar d / r ?”

Bem, porque r é muito grande de fato, mas d / r ainda não é tão insiginificante quanto é d 2 / r 2 , ta ligado?

Com esse termo aí, a gente vai simplificar também, mas de outra maneira!

Passo 5

POW! A matemática tem uma simplificação que é muito massa e útil para esses casos! Ela fala o seguinte: se a é um número muito menor que 1 e próximo de 0 , então podemos fazer a seguinte simplificação...

1 - a c ≅ 1 - c   a

No nosso caso, o termo d r cos ⁡ θ é um número muito pequeno (bem menor que 1 ) então...

V = q 4 π ε 0 1 r 1 - d r cos ⁡ θ - 1 / 2 - 1 r 1 + d r cos ⁡ θ - 1 / 2   →

V = q 4 π ε 0 1 r 1 + d 2 r cos ⁡ θ - 1 r 1 - d 2 r cos ⁡ θ   →

Simplificando agora...

V = q 4 π ε 0 1 r + d 2 r 2 cos ⁡ θ - 1 r + d 2 r 2 cos ⁡ θ   →

V = q 4 π ε 0 2 d 2 r 2 cos ⁡ θ   →

V = q 4 π ε 0 d r 2 cos ⁡ θ

Prontinho! Essa é a expressão para o potencial muito longe das cargas

Passo 6

L e t r a   C :

Bem... Sabemos ser o campo elétrico o gradiente do potencial...

E → = - ∇ V

Como temos um potencial em coordenadas polares (em termos de r e θ ), acho legal a gente escrever a expressão do gradiente nas coordenadas polares! Que é de acordo com a teoria...

E → = ∂ V ∂ r   r ^ + 1 r ∂ V ∂ θ   θ ^     →

Onde r ^ é o vetor unitário na direção de r e θ ^ na direção de θ (são versores). Substituindo a expressão de V ...

E → = ∂ ∂ r q 4 π ε 0 d r 2 cos ⁡ θ   r ^ + 1 r ∂ ∂ θ q 4 π ε 0 d r 2 cos ⁡ θ   θ ^     →

E → = q d cos ⁡ θ 4 π ε 0   ∂ ∂ r 1 r 2   r ^ + q d 4 π ε 0 r 3   ∂ ∂ θ cos ⁡ θ   θ ^     →

Derivando...

E → = q d cos ⁡ θ 4 π ε 0   - 1 r 3   r ^ + q d 4 π ε 0 r 3   ∂ ∂ θ - sin ⁡ θ   θ ^     →

E → = - q d cos ⁡ θ 4 π ε 0 r 3     r ^ - q d 4 π ε 0 r 3   sin ⁡ θ   θ ^  

Resposta

Letra A:

V = q 4 π ε 0 1 r + - 1 r -

Letra B:

V = q 4 π ε 0 d r 2 cos ⁡ θ

Letra C:

E → = - q d cos ⁡ θ 4 π ε 0 r 3     r ^ - q d 4 π ε 0 r 3   sin ⁡ θ   θ ^

Exercícios de Livros Relacionados

Duas partículas com a mesma carga positiva q são mantidas fixas no eixo y, uma em y =d e a outra em y = - d. (a) Escreva uma expressão para o módulo E do campo elétrico em pontos do eixo x dados por x
Três cargas se situam nos vértices de um triângulo isósceles, como indica a figura 21.43. As cargas de ± 5μ C formam um dipolo.(a) Determine a força (módulo, direção e sentido) que a carga - 10μ C exe
Um dipolo elétrico é submetido a um campo elétrico uniforme E → de módulo 40N/C. A Fig. 22-58 mostra o módulo τ do torque exercido sobre o dipolo em função do ângulo θ entre o campo E → e o momento di
Uma molécula tem um dipolo dado por p → . A molécula está momentaneamente em repouso com p → fazendo um ângulo θ com um campo elétrico uniforme E → . Descreve o movimento subsequente do momento de dip
Um dipolo elétrico que tem momento de dipolo p → está localizado a uma distância perpendicular R de uma linha infinitamente longa de cargas que tem densidade linear uniforme λ . Considere que o moment