Determine os parâmetros geométricos , e da elipse que tem focos e e cujo eixo maior mede 10. Faça um esboço exibindo as coordenadas dos vértices.
Passo 1
O eixo maior é dado por lembra? Então
Já temos um parâmetro :D
O parâmetro é a metade da distância entre os focos:
Podemos encontrar o parâmetro pela relação
Então nosso esboço fica assim
Resposta
Exercícios de Livros Relacionados
Mostre que a equação da reta tangente à elipse x 2 a 2 + y 2 b 2 = 1 no ponto x 0 ,y 0 da elipse é x 0 x a 2 +y 0 y b 2 = 1 .
Nos problemas de 34 a 39, obter equações paramétricas da elipse de equação dada 9 ( x - 1 ) 2 + 25 ( y + 1 ) 2 = 225
Nos problemas de 40 a 43, obter uma equação geral da elipse dada por equações paramétricas. x = cos θ y = 3 . s e n θ
Nos problemas de 34 a 39, obter equações paramétricas da elipse de equação dada 49 ( x + 7 ) 2 + y ² = 7 ²
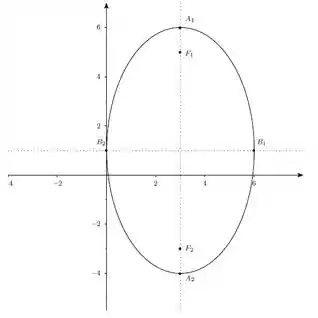
Em cada um dos Problemas de 20 a 27, obter uma equação da elipse que satisfaça as condições dadas.Centro C ( 2 , - 1 ) , tangente aos eixos coordenados e eixos de simetria paralelos aos eixos coordena