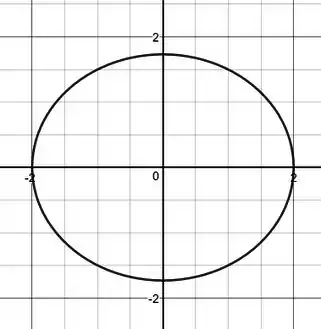
Para as elipses dadas, determine os vértices, os focos, a excentricidade . Faça um esboço.
Passo 1
Bora começar a aquecer nossos neurônios sobre elipses!! Hehe
Temos quatro itens cada um com uma expressão de uma elipse e em cada item devemos determinar: vértices, focos, excentricidade e fazer um esboço.
Vamos comerçar!!

Passo 2
a)
Para começarmos esse exercício precisamos colocar a expressão na forma reduzida, ou seja, desse jeito:
Porque assim conseguiremos determinar os valores de e que precisamos para achar os elementos que queremos.
Então, vamos começar!!
Dividindo tudo por , temos:
Como deve ser sempre maior que , então:
Como deve ser maior que e está embaixo do então significa que estamos no caso 1, e teremos uma elipse com o seguinte formato:
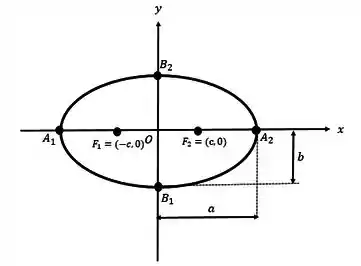
Pela figura, conseguimos determinar os focos e vértices
Temos o valor de e , mas para determinar os focos precisamos de . Mas, como vamos achar ?
Para achar vamos usar a seguinte relação das elipses: . Subsituindo os valores de e , temos:
Repare que o resultado seria , porém como e são distânciasnão faz sentido o valor negativo.
Agora sim, temos tudo o que precisamos é só substituir os valores e encontrar os focos, vértices e excentricidade.
E fazendo um esboço, temos:
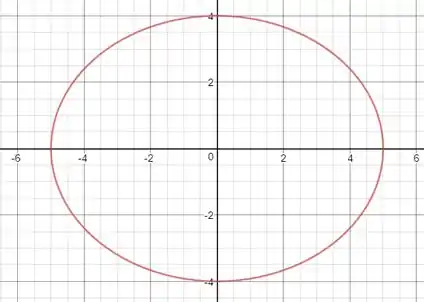
Passo 3
b)
O passo a passo é o mesmo do item anterior, começamos escrevendo na forma canônica:
Como o maior denominador está sobre o teremos a elipse do mesmo jeito do caso anterior, ou seja, caso 1:
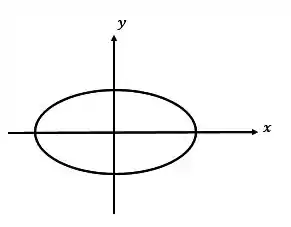
Sendo o maior valor , então:
Utilizando a relação :
Substituindo esses valores a seguir:
Subsituindo, temos:
Esboçando:
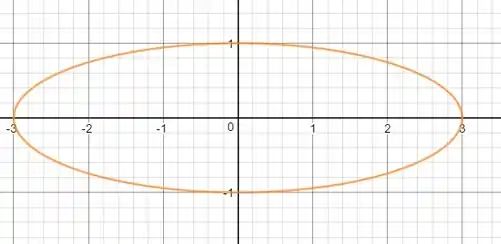
Passo 4
c)
Colocando na forma canônica:
Agora, o maior valor do denominador está dividindo o . Isso indica que estamos no CASO 2, assim nossa elipse terá o seguinte formato:
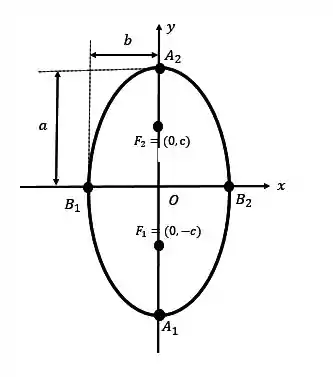
Sabendo que nossa elipse é assim, sabemos que nossos focos e vértices, serão:
Para determina-los precisamos calcular e .
Para encontrar esses valores continuamos a fazer o mesmo procedimento. Assim, o valor de é sempre referente ao maior denominador que é , então:
Usando a relação que é válida para qualquer elipse, temos:
Agora, podemos achar focos, vértices e a excentricidade:
Esboçando:
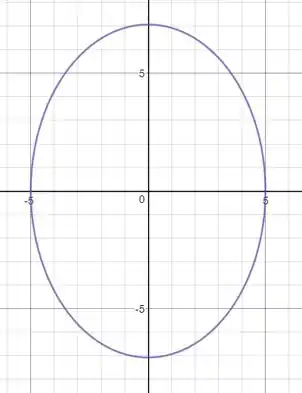
Passo 5
Ufa!! Só falta mais uma!! Uhuuulll
d)
Colocando na forma canônica:
O maior valor do denominador está devidindo o , logo estamos no CASO 1:
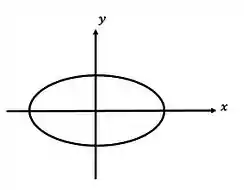
Então, nossos valores de e são:
Tendo os focos, vértices e excentricidade em função de e , temos:
Substituindo:
Para finalizar falta esboçar!!
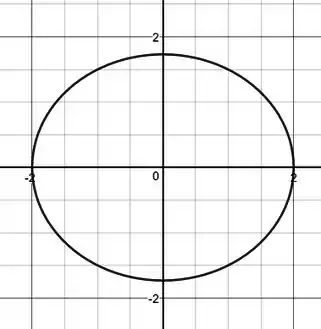
Terminamooossss!!!

Resposta
a)
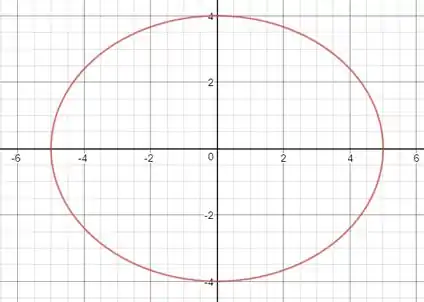
b)
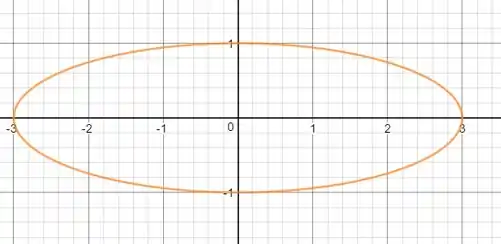
c)
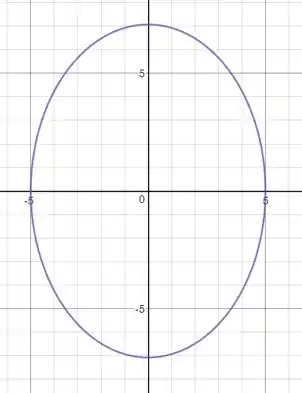
d)