Encontre a equação reduzida de um elipse que têm focos num dos eixos de coordenadas e centro na origem, sabendo que os pontos e pertencem a esta elipse.
Especifique as coordenadas dos focos e calcule a excentricidade. Desenhe.
Passo 1
Para podermos identificar as coordenadas dos focos, calcular a excentricidade e desenhar a elipse, precisamos calcular a equação reduzida da nossa elipse.
Vamos lá. Sabemos que ela possui focos em algum dos eixos coordenados, ou seja, sobre o eixo ou eixo . Portanto, ela não está transladada. Sendo assim, a equação reduzida da elipse possui a seguinte forma:
Só que a elipse está centrada na origem. Então, as coordenadas do seu centro são . Logo, a sua equação reduzida é dada por:
Agora, nosso trabalho é identificar os valores de e . E a chave para isto está nos dados da questão! Ela não nos forneceu as coordenadas de dois pontos que pertencem a elipse?
Então, se estes pontos pertencem a elipse, é porque eles satisfazem a sua equação! Isto quer dizer que podemos substituir as coordenadas do ponto na equação. Começando pelo ponto , temos
Identificamos o primeiro parâmetro geométrico! Percebam que pegamos apenas o valor positivo pois todos os parâmetros geométricos são positivos por definição! Sendo assim, a nossa equação pode ser reescrita da seguinte forma:
Continuando, para descobrir o valor de , basta substituir as coordenadas do segundo ponto . Portanto,
Novamente, é fundamental destacar que o parâmetro geométrico é positivo por definição!!! Finalizando uma parte da questão, temos que a equação reduzida da elipse é:
Passo 2
Agora que obtivemos a equação reduzida da elipse, podemos partir para a identificação dos outros parâmetros que a questão nos pede.
Primeiro, vamos para as coordenadas do foco. A questão já nos disse que eles estão localizados em algum dos eixos coordenados. Então, ou são dados por ou , a depender se estão no eixo ou , respectivamente.
E então, como identificamos? Basta olhar o maior denominador na equação reduzida da elipse. Isto sempre será verdade para uma elipse centrada na origem e com foco em algum dos eixos. Como o maior denominador é 16, que está dividindo , isto significa que os focos estão no eixo !
Pronto! Quase lá. Falta encontrarmos o valor de . Para uma elipse, ele é dado por:
Lembrando que esse e são os parâmetros geométricos e que calculamos no passo anterior (não nesta ordem). O parâmetro é o maior valor (que no caso corresponde a ) e o parâmetro corresponde ao menor valor (que neste caso corresponde a ).
Continuando as contas, temos:
Portanto, os focos estão localizados nos pontos e
Passo 3
A excentricidade de uma elipse é obtida diretamente da divisão dos parâmetros geométricos e . Portanto,
OBS: é importante destacar que a excentricidade de uma elipse SEMPRE está na faixa . Qualquer valor diferente deste significa que erramos nas contas!
Passo 4
Para finalizarmos a questão, vamos esboçar a elipse. Utilizando softwares para nos ajudar neste plot, temos:
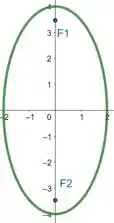
Percebam que a elipse corta o eixo nos pontos . E este valor é exatamente o valor de descoberto anteriormente. Da mesma forma acontece com o eixo . A elipse corta este eixo em .
E também, como era esperado, os focos estão no eixo (os focos estão no eixo maior da elipse, basta olhar qual a direção que ela está mais achatada).
Resposta
A equação reduzida da elipse é:
As coordenadas dos focos são e . A excentricidade é .
O esboço da elipse é: