(Adaptada) Um tubo de aço de paredes finas com de diâmetro é utilizado para transportar vapor saturado a uma pressão de através de um ambiente onde a temperatura do ar é e o coeficiente de convecção na superfície externa do tubo é . A resistência convectiva do lado vapor pode ser desprezível.
Qual é a perda de calor por unidade de comprimento para o tubo sem isolamento? A emissividade do aço pode ser considerada .
Encontre a equação que descreve a temperatura da superfície externa do isolamento em função dos parâmetros conhecidos (polinômio de quarto grau) se uma camada de isolamento térmico ( e ) com de espessura for aplicada ao redor do tubo.
Após resolver o polinômio de quarto grau, você achou uma temperatura de . Estime a perda de calor com o isolamento.
Passo 1
Qual é a perda de calor por unidade de comprimento para o tubo sem isolamento? A emissividade do aço pode ser considerada .
Sem o isolamento, a gente tem a situação simples de uma casca cilíndrica envolvida por um grande ambiente e que sofre convecção externa. Esquematizando, fica mais ou menos assim:
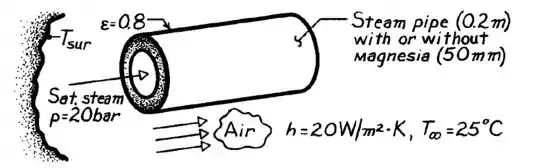
Como o enunciado diz que o vapor é saturado, com a pressão que foi dada podemos achar sua temperatura em uma tabela de propriedades da água saturada, encontrando .
Considerando então que a resistência de convecção interna é desprezível, a gente pode assumir que a temperatura da superfície interna da casca cilíndrica é igual à temperatura do vapor.
E, como a parede do tubo é fina, também desprezamos a resistência por condução, logo a temperatura da superfície externa também equivale a .
Bora fazer um balanço de energia na superfície do tubo, que é onde a energia é dissipada pro ambiente:
Em que a perda de calor é dada pela soma dos calores de convecção e radiação. Ou seja, calcular a perda de calor equivale a calcular quanto entra de calor na superfície ().
Bora calcular cada uma das taxas! Para a taxa de convecção:
Escrevendo em termos da taxa por unidade de comprimento, a gente fica com:
Para a taxa de radiação:
Assim como fizemos antes:
OBS: Você também pode escrever as taxas em função das resistências, mas, se você lembrar, a expressão da resistência de radiação é bem feiosa. Então, geralmente quando trabalhamos com radiação, é mais fácil usar direto a expressão das taxas.
Dessa maneira, a gente pode já substituir as taxas encontradas:
Passo 2
Encontre a equação que descreve a temperatura da superfície externa do isolamento em função dos parâmetros conhecidos (polinômio de quarto grau) se uma camada de isolamento térmico ( e ) com de espessura for aplicada ao redor do tubo.
Se aplicarmos uma camada de isolante em volta da casca cilíndrica, estaremos adicionando uma resistência de condução no sistema, como mostrado abaixo:
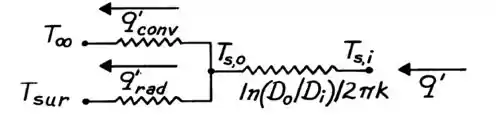
Como a gente não conhece as temperaturas, precisamos encontrar alguma delas pra poder calcular a taxa!
Ao fazermos o balanço de energia na superfície mais externa (que agora é a superfície externa do isolamento), teremos o seguinte:
Substituindo as expressões para a resistência térmica em paredes cilíndricas () e a área de troca térmica ()
Pronto! Note que a equação acima é um polinômio de quarto grau em e que todos os outros parâmetros dela são conhecidos!
Passo 3
Sabendo que a temperatura da superfície externa do isolamento equivale a , a gente pode calcular a taxa de calor de condução, pois ela representa a mesma quantidade de energia que é perdida pelo tubo por convecção e radiação.
Temos que:
A resistência de condução na parede cilíndrica pode ser calculada por:
Então:
Substituindo na expressão da taxa de calor:
Como não sabemos o comprimento do tubo, a gente pode simplesmente determinar a taxa de calor por unidade de comprimento ():
Logo, a perda de calor também será:
Resposta