(Adaptada) Um tanque esférico para armazenar oxigênio líquido no ônibus espacial deve ser construído em aço inoxidável () com de diâmetro e de espessura de parede. O ponto de ebulição e o calor latente de fusão do oxigênio líquido são e respectivamente. O tanque será instalado em um grande compartimento cuja temperatura deve ser mantida a . Projete um sistema de isolamento térmico capaz de manter as perdas de oxigênio por evaporação abaixo de . Admita que a condutividade do isolamento equivale a e considere a resistência de convecção desprezível frente às demais resistências térmicas.
Passo 1
Nosso objetivo nessa questão é projetar um sistema de isolamento para uma esfera, isso significa que a gente tem que determinar qual a espessura do isolamento vamos usar pra revestir o tanque esférico.
A situação pode ser esquematizada da seguinte forma:
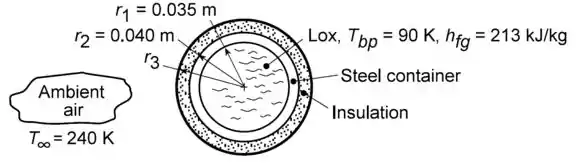
O sistema de isolamento deve ser tal que a taxa de evaporação do oxigênio líquido seja inferior a . “Mas o que isso tem a ver?”
A gente sabe que dada uma pressão fixa, a gente pode evaporar líquido fornecendo uma certa quantidade de energia, certo?
Então, a gente consegue relacionar a taxa de evaporação com a taxa de calor do sistema, dá uma olhadinha:
Essa é a equação do calor latente (), ou seja, a quantidade de energia pra evaporar a substância. Ele é função da quantidade de massa que evapora () e do calor latente de ebulição da substância em questão ().
Só que aqui a gente tá trabalhando com taxa, então bora dividir os dois lados da equação por :
Assim a gente fica com a taxa de calor () e com a taxa mássica de evaporação ():
Beleza! Então, se a gente precisa projetar um isolamento pra que a taxa de evaporação seja menor que , é a mesma coisa que projetar o isolamento pra uma taxa de calor menor que:
Beleza, agora já ficou um pouco melhor! O enunciado passa a ser “Projete um sistema de isolamento térmico para que a taxa de calor seja menor que ”.
Passo 2
Agora, a gente tem que calcular qual a espessura de isolamento que permite a passagem de somente . Bora lá!
A gente pode construir um circuito térmico considerando as paredes de aço () e de isolamento () mais a resistência de convecção externa ():
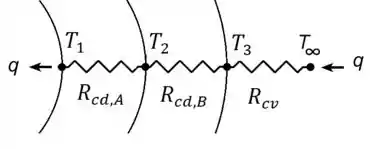
A gente pode escrever a equação para a taxa da seguinte maneira:
Note que, projetar a espessura de isolamento é o mesmo que determinar o valor de !
Bora encontrar o valor da resistência total primeiro:
Passo 3
Como as resistências estão em série, podemos escrever a resistência total como:
Mas, pelo enunciado, a gente pode desprezar a resistência de convecção, então:
Em que as resistências são dadas por:
Bora calcular a resistência do aço:
Passo 4
Beleza, então a gente pode escrever que:
Substituindo o que calculamos:
Viu que a resistência de condução é tão baixinha que não fez nem cócegas na resistência total? Pois é!
Abrindo a expressão da resistência de condução no isolamento, a gente fica com:
Logo:
Dessa forma:
Passo 5
Isso significa que a espessura de isolamento é dada por:
Ou seja: