Uma corrente elétrica de flui através de um cabo de aço inoxidável de diâmetro e resistência elétrica de (ou seja, por metro de comprimento de cabo). O cabo encontra-se em um ambiente que está a uma temperatura de , e o coeficiente total de transferência de calor, associado à convecção entre o cabo e o ambiente, é de aproximadamente .
Se o cabo estiver desencapado, qual será a temperatura em sua superfície?
Se um revestimento delgado for aplicado sobre o cabo, com uma resistência térmica de contato de , quais serão as temperaturas das superfícies do isolamento e do cabo?
Há preocupação em relação à capacidade do isolamento em suportar temperaturas elevadas. Qual a espessura do isolamento () que produzirá o menor valor para a temperatura máxima na camada de isolamento? Qual será o valor da temperatura máxima quando essa espessura de isolamento for utilizada?
Passo 1
Se o cabo estiver desencapado, qual será a temperatura em sua superfície?
Nosso primeiro desafio é o mais simples: a gente tem que calcular a temperatura no fio sem isolamento algum, ou seja, é só um corpo cilíndrico com geração de calor!
Como passa uma corrente elétrica pelo fio, a gente já sabe que vai gerar energia térmica () pelo efeito Joule. Então, bora escrever a expressão do fluxo de calor:
O enunciado não nos deu a informação quanto à resistência elétrica () do fio, mas sim a resistência por unidade de comprimento do fio (). Então, a gente pode escrever a taxa de calor gerada em termos do comprimento também:
Ou a gente pode fazer tudo em termos de taxa de calor, que depois o comprimento vai cortar! Essa é sempre uma boa estratégia, então vamos fazer isso!
Escrevendo em termos da taxa:
Passo 2
Com a taxa de calor já calculada, bora fazer um balanço de energia na superfície do fio:
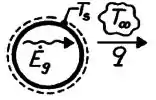
Então, conseguimos perceber que a energia gerada no volume do cilindro () entra na superfície externa e ela é dissipada por convecção.
Dessa maneira, a gente fica com o seguinte balanço de energia na superfície:
Fazendo um circuito térmico simples, temos:
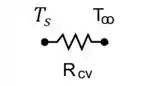
Substituindo a expressão da taxa por convecção (), a gente fica com:
Como a gente quer determinar a temperatura da superfície, bora isolar o termo :
Com a expressão da resistência , teremos:
Substituindo os valores do enunciado, a gente fica com:
Viu como cortou o comprimento do fio! ^^ Agora é só fazer os cálculos e:
Passo 3
Se um revestimento delgado for aplicado sobre o cabo, com uma resistência térmica de contato de , quais serão as temperaturas das superfícies do isolamento e do cabo?
Na nova situação, a gente vai pegar aquele mesmo fio da letra a) e vamos colocar um isolamento envolvendo sua superfície.
Daí você poderia pensar que ao colocar o isolamento, a gente iria ficar com um circuito térmico da seguinte maneira:
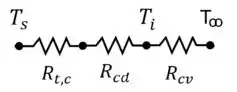
Tá certo! Mas aqui, o isolamento é delgado, ou seja, ele é muito, muito, muito fino!
Como a gente sabe, quanto menor a espessura do material, menor será a resistência térmica dele. Então, para um isolamento delgado, a resistência por condução dele será desprezível, ficando, então, só a contribuição da resistência de contato!
Sendo assim, o circuito adequado seria:
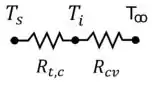
Fazendo novamente o balanço de energia na superfície do fio, a gente fica com uma expressão parecida com a que achamos na letra a):
Mas agora existe uma resistência térmica de contato em série com a de convecção!
Isolando a temperatura da superfície do fio, a gente fica com:
Mas cuidado!! A gente não pode colocar direto aquele valor de resistência térmica de contato do enunciado! Aquele valor é a resistência por unidade de área ()! Pra gente converter um no outro, basta dividir pela área de troca térmica:
Assim:
Substituindo os valores do enunciado:
Dessa maneira, a temperatura da superfície do fio será:
Passo 4
Ainda temos que calcular a temperatura da superfície do isolamento. Então, ao invés de pegar todo o circuito, bora pegar só a parte da convecção!
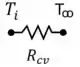
Assim, nossa equação vai ficar:
Isolando a temperatura do isolamento, ficamos com:
Substituindo os valores:
Hm, tá lembrado desse número!? Pois é, foi o mesmo valor que a gente achou na letra a). E já era de se esperar, porque estamos calculando a temperatura de um cilindro exposto ao mesmo fluido, com a mesma temperatura e com a mesma taxa de energia gerada.
Mas isso, claro, só porque o isolamento é delgado. “Mas e se ele não fosse?”. É isso que vamos ver na letra c), pequeno gafanhoto! Bora lá!
Passo 5
Há preocupação em relação à capacidade do isolamento em suportar temperaturas elevadas. Qual a espessura do isolamento () que produzirá o menor valor para a temperatura máxima na camada de isolamento? Qual será o valor da temperatura máxima quando essa espessura de isolamento for utilizada?
Agora sim! Aquele circuito térmico com a resistência de condução do isolamento vai aparecer aqui! Se liga aí:
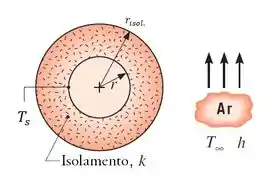
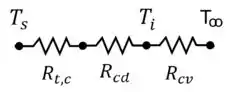
Então, a gente pode fazer o mesmo esquema que fizemos nas letras a) e b). Então, ao balanço de energia e além...
Agora, a gente tem a resistência de condução em série com as resistências de contato e de convecção! Isolando a temperatura da superfície do fio:
Com as expressões da resistência, ficamos com:
Mas agora temos um pequeno desafio: a gente não sabe nem a temperatura da superfície (), nem a espessura do isolamento (), pra poder calcular a resistência de condução. O que fazer?
Passo 6
O enunciado nos pediu uma coisa: a espessura do isolamento que produzirá o menor valor para a temperatura máxima na camada de isolamento.
Você já aprendeu no cálculo como encontrar máximo e mínimos, não é mesmo? Pois é, então aqui a gente pode achar qual é o valor de que faz a derivada de zerar!
Derivando a expressão que achamos em função de , teremos:
No ponto de mínimo, a derivada é nula:
Assim:
Ou seja, o raio do isolamento equivale a:
Assim, a espessura do isolamento será:
Passo 7
Agora que já descobrimos a espessura do isolamento, podemos determinar as temperaturas da superfície do fio e do isolamento.
Pela expressão que achamos da temperatura na superfície do fio:
Pelos cálculos, ficamos com:
Essa será a temperatura máxima do Sistema, dado que ela se refere a superfície mais próxima à geração de calor (que ocorre no interior do fio).