Um vaso esférico de aço inoxidável , com de diâmetro interno e de espessura de parede, é usado como reator químico.
A superfície externa do reator é resfriada por ar com temperatura de e coeficiente de transferência de calor de . No regime permanente, deseja-se saber.
Qual a taxa de calor transferida para o ar, sabendo-se que a temperatura da superfície interna do vaso e de ?
Qual a taxa volumétrica média de geração de energia no interior do reator?
Utilizando a taxa de geração de energia calculada no item e supondo que uma camada de de espessura de fibra-de-vidro seja usada para isolar o reator, responda qual é a temperatura da superfície interna do reator. O contato entre o isolante e parede do reator é suposto perfeito.
Passo 1
Qual a taxa de calor transferida para o ar, sabendo-se que a temperatura da superfície interna do vaso e de ?
Como temos as temperaturas do ar externo e da superfície interna do vaso, a taxa de transferência de calor pode ser calculada a partir do seguinte circuito térmico.
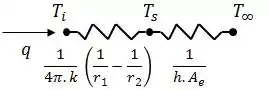
Onde . Assim, a taxa de calor será:
Substituindo os valores:
![]()
Passo 2
Qual a taxa volumétrica média de geração de energia no interior do reator?
A taxa de geração pode ser calculada da seguinte forma:
![]()
Passo 3
Utilizando a taxa de geração de energia calculada no item e supondo que uma camada de de espessura de fibra-de-vidro seja usada para isolar o reator, responda qual é a temperatura da superfície interna do reator. O contato entre o isolante e parede do reator é suposto perfeito.
Ao adicionar a camada de fibra de vidro, o circuito térmico passa a ser dado por:
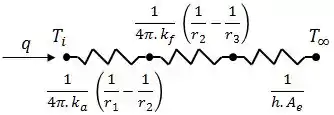
A resistência térmica total do circuito será dada por:
Como o problema nos pede pra usar a mesma taxa de geração de energia, ele na verdade está falando pra considerarmos a mesma taxa de calor que calculamos no item . Dessa forma, a temperatura da superfície interna será:
![]()
Resposta