Uma casca esférica composta, com raio interno é construída de chumbo () de raio externo e aço inoxidável () de raio externo . A cavidade é preenchida com resíduos radioativos que geram calor a uma taxa de . Propõe-se que o recipiente seja submerso em águas oceânicas que estão a uma temperatura e fornecem um coeficiente de convecção uniforme para a superfície externa do contêiner. Existe algum problema associado a essa proposta?
Admita que a temperatura de fusão dos materiais são: e .
Passo 1
Você deve ter se perguntado: “Como assim ‘algum problema associado à proposta’?” Então, muitas vezes em processos de transferência de calor, a gente tá interessado em saber se um sistema “aguenta” a quantidade de calor gerada, ou seja, se alguma peça vai derreter.
Sabendo disso, nosso objetivo nessa questão é calcular as temperaturas de cada superfície e garantir que elas não ultrapassem os pontos de fusão do respectivo material.

Agora que sabemos o que fazer, bora dar uma olhadinha num esquema da situação:
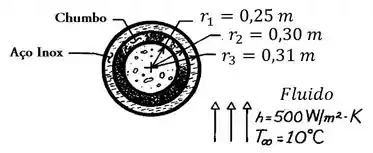
Como não há geração na casca esférica composta em si, a gente pode construir o circuito térmico representativo do sistema:
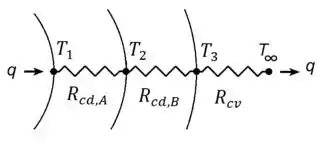
Em que as resistências de condução em geometrias esféricas têm uma expressão diferente da placa plana e das geometrias cilíndricas:
Passo 2
Pelo circuito, a gente pode escrever que:
A gente viu que a fonte calor desse sistema são os resíduos radioativos no interior da cavidade, que geram uma taxa volumétrica de .
Então, para achar a taxa de calor que flui pela esfera até o ambiente, basta a gente multiplicar pelo volume da cavidade:
Dessa forma:
Passo 3
Então, só nos resta calcular as resistências no circuito térmico que fizemos!
Para a condução no chumbo:
Para a condução no aço inoxidável:
Calculando ainda a resistência de convecção:
Passo 4
Substituindo na expressão da taxa, teremos:
Isolando a temperatura da superfície , a gente fica com:
Passo 5
Como é a temperatura na superfície do chumbo e seu valor é menor que o da temperatura de fusão desse material (), então o chumbo não vai derreter ali.
Mas e as demais temperaturas ( e )? Temos que calculá-las pra saber se os materiais vão derreter? Não! “Mas por quê?”
Note que é a maior temperatura do sistema, pois ela é a temperatura da superfície mais próxima da região onde a energia é gerada. Então:
Se o chumbo não derrete na maior temperatura do sistema (), então ele também não derreterá na superfície mais externa (a temperatura de ).
E o aço? A temperatura de fusão do aço é de (ou ), que é bem maior que e, consequentemente, também será maior que e . Logo, ele também não derreterá!
Resposta
Não há nenhum problema associado ao derretimento das peças utilizadas no sistema.
Nenhuma temperatura das superfícies supera os pontos de fusão do aço e do chumbo!